In this code below, I’m using the brfharness module I created. You can find it on this page. It simplifies the setup of one or more BladeRF cards to keep all the boilerplate code to a minimum.
I wanted to do some work with phase comparisons. I created two signals. A linear chirp and a constant power single frequency. I made the chirp about 0.25-seconds in my test and the single frequency should be almost continuous as has some abrupt change in phase at the end of one second since it wasn’t an integer multiple. I put my chirp at 50khz to 70khz and the signal at 10khz. I also added one additional signal at 20khz.
# transmitter command line
LD_LIBRARY_PATH=/home/outpost/bladeRF/host/build/output python3 search.py --serial 9da --freq 1.83e9 --sps 520834 --tx --chirp-start 50e3 --chirp-end 70e3 --chirp-length 0.25 --local-freq-a 10e3 --local-freq-b 20e3
# receiver command line
LD_LIBRARY_PATH=/home/outpost/bladeRF/host/build/output python3 search.py --serial 9da --freq 1.83e9 --sps 520834 --chirp-start 50e3 --chirp-end 70e3 --chirp-length 0.25 --local-freq-a 10e3 --local-freq-b 20e3
I then found the offset of the chirp using a correlation in receiver mode. You can see from the program below the switch from transmit to receiver mode is done with the command line argument --tx.
The curious case is that the phase isn’t stable for the chirp nor the single frequency! Neither one has any correlation that I can find either. It would seem to me that the chirp and the single frequency should hold a steady phase but instead they appear to both randomly jump about in different directions.
I should mention that I do the test on two different boards and maybe this is the origin of the problem.
import argparse
import brfharness
import argparse
import numpy as np
import scipy.signal as signal
import pickle
def entry(cards, sps, freq, buffer_samps, args):
samps = sps
t = samps / sps
assert args.chirp_length > 0 and args.chirp_length <= 1.0
csr = args.chirp_start * np.pi * 2 / sps
cer = args.chirp_end * np.pi * 2 / sps
csamps = int(sps * args.chirp_length)
chirp = np.exp(1j * np.add.accumulate(np.linspace(csr, cer, csamps)))
sig0 = np.exp(1j * np.linspace(0, np.pi * 2 * args.local_freq_a * t, samps))
sig1 = np.exp(1j * np.linspace(0, np.pi * 2 * args.local_freq_b * t, samps))
if args.tx:
# non-chirp signal should stay at about 50% power all the way even
# though the chirp may end sooner; constant power
tx_data0 = sig0 + sig1
tx_data0[0:len(chirp)] += chirp
tx_data0 /= np.max(np.abs(tx_data0))
tx_data0 *= 2000
tx_data2 = np.zeros((len(tx_data0) * 4), np.int16)
tx_data2[0::4] = tx_data0.real
tx_data2[1::4] = tx_data0.imag
tx_data2[2::4] = 0
tx_data2[3::4] = 0
tx_data = tx_data2.tobytes() * 10
cards[0].set_tx_data(tx_data)
cards[0].set_tx_gain(30)
input('Press Enter To Stop')
cards[0].exit()
else:
# Flush the junk from start-up that is in the buffers.
_, sa, sb = cards[0].get_samples(sps)
delta = 2e3
sig_sos_a = signal.butter(
32,
(args.local_freq_a - delta, args.local_freq_a + delta),
btype='bandpass',
output='sos',
fs=sps
)
sig_sos_b = signal.butter(
32,
(args.local_freq_b - delta, args.local_freq_b + delta),
btype='bandpass',
output='sos',
fs=sps
)
last = []
last_cor = []
sol = 299792458
while True:
rx_counter, sa, sb = cards[0].clear_buffer_get_samples(sps)
print('sa', np.mean(np.abs(sa)))
chirp_cor_c = signal.correlate(sa, chirp, mode='valid')
chirp_cor = np.abs(chirp_cor_c)
ndx = np.argmax(chirp_cor)
if chirp_cor[ndx] < 2000:
print('miss')
continue
left = len(sa) - ndx
# extract just signal 0 (sinusodial)
sc0 = signal.sosfiltfilt(sig_sos_a, sa)
# extract just signal 1 (sinusodial)
sc1 = signal.sosfiltfilt(sig_sos_b, sa)
# compute signal0 actual approx. frequency
ta0 = np.angle(np.sum(sc0[1:] * np.conjugate(sc0[:-1])))
ta0_freq = ta0 * sps / (np.pi * 2)
# compute signal1 actual approx. frequency
ta1 = np.angle(np.sum(sc1[1:] * np.conjugate(sc1[:-1])))
ta1_freq = ta1 * sps / (np.pi * 2)
# compute the phase error from what it was at the TX antenna for
# both signals
t = left / sps
qq0 = np.exp(1j * np.linspace(0.0, np.pi * 2 * ta0_freq * t, left))
qqr0 = np.sum(qq0 * np.conjugate(sc0[ndx:]))
qq1 = np.exp(1j * np.linspace(0.0, np.pi * 2 * ta1_freq * t, left))
qqr1 = np.sum(qq1 * np.conjugate(sc1[ndx:]))
# compute the amount of phase error of the chirp
last_cor.append(chirp_cor_c[ndx])
last_cor_sum = np.sum(last_cor)
last_cor_theta = np.angle(last_cor_sum) / np.pi * 180
last_cor_mag = np.abs(last_cor_sum)
# try to calculate the distance between the antennas
last_cor_dist = last_cor_theta / 180.0 * np.pi / (np.pi * 2) * (sol / freq) * 3.2808399 * 12
# compute the stability of the phase error between the two signals
last.append(qqr0 * np.conjugate(qqr1))
last_sum = np.sum(last)
last_theta = np.angle(last_sum) / np.pi * 180
last_mag = np.abs(last_sum)
print(f'dist:{last_cor_dist:.1f}-inches chirp:{last_cor_theta:.1f}[{last_cor_mag:.0f}] diff:{last_theta:.0f}[{last_mag:.0f}]')
def main(args):
if args.tx:
initial_tx_gain = 30
else:
initial_tx_gain = -24
cards, buffer_samps = brfharness.setup([args.serial], args.sps, args.freq, initial_tx_gain)
entry(cards, args.sps, args.freq, buffer_samps, args)
if __name__ == '__main__':
ap = argparse.ArgumentParser()
ap.add_argument('--serial', type=str, required=True)
ap.add_argument('--freq', type=float, required=True)
ap.add_argument('--local-freq-a', type=float, required=True)
ap.add_argument('--local-freq-b', type=float, required=True)
ap.add_argument('--chirp-start', type=float, required=True)
ap.add_argument('--chirp-end', type=float, required=True)
ap.add_argument('--chirp-length', type=float, required=True)
ap.add_argument('--tx', action=argparse.BooleanOptionalAction, default=False)
ap.add_argument('--sps', type=int, required=True)
main(ap.parse_args())In the above code, I try to calculate the amount the phase has shifted in order to determine the distance. I hoped to use the chirp offset to denote what should be roughly phase zero for the signals. I then try to perform an average over the long-term to eliminate any noise.
The results are mixed from the average. On one hand, it appears that it tries to converge to the right answer, but it also has a lot of error which makes it difficult to tell if I have the computation right.
If you plot the output, you can see that it tries to converge to a single value. In my test the antennas are about 11-inches apart – give or take less than an inch.
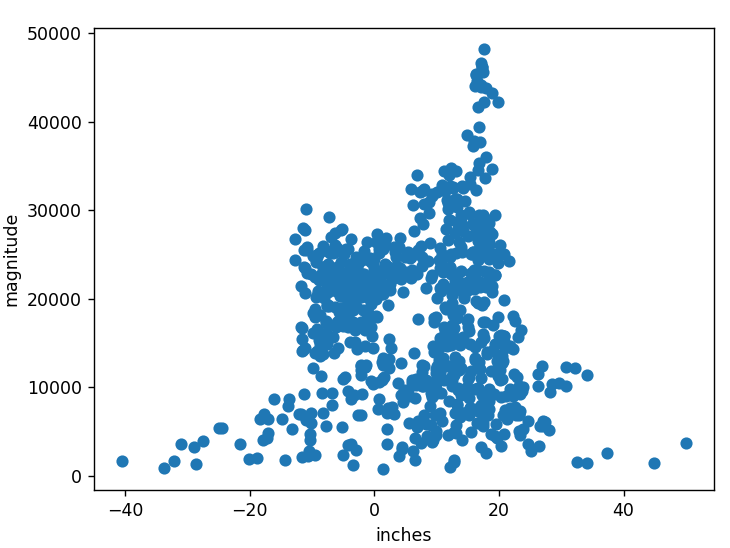
The problem is that the value the test appeared to converge toward was 18-inches which would be incorrect – but close.
Same Card
Now, if I use the same card. I simply remove the else condition and immediately run the RX routine then I can get a stable phase output from the chirp at the least. This says to me that the problem is in using the two different cards and the biggest difference in the cards would be the minute sampling rate difference. If I am correct, I only need to find a way to correct the sampling rates.
New Findings
Now, I was using a chirp to try to find a specific point in time. I abandoned the chirp and decided to use a phase reversal. But as an additional change I made sure that for the phase reversal each of the three signals was crossing the zero point. I figured too that the mixer will impact its own spin so the absolute phase will be a toss-up unless I was able to calculate that – which might be possible, I just did not. However, in previous tests I was unable to get a stable relative phase difference at a known point for which I can only believe the chirp was simply not very accurate in position.
I used three signals because trying to use two signals resulted in doing a phase transition and it seemed to distort the waveform enough the measurement might have suffered. This caused me to use three signals.
My three signals were 4khz, 12khz, and 26khz using the --local-freq-* parameters. These seemed to work well and had a good lock.
Using the phase reversal method I get a somewhat stable phase difference which should be a function of distance. This would be because each wavelength has a different phase velocity meaning not only does the mixer impart a spin (phase rotation) but the mixer should impart an equal spin to each frequency. The propagation should impart a spin (phase rotation) dependent on frequency meaning the two signals arrive out of phase not because of the mixer but because of propagation of the wave.
Here is the same program but re-written to do the above. It should measure that phase difference from the travel distance.
import argparse
import brfharness
import argparse
import numpy as np
import scipy.signal as signal
import pickle
def entry(cards, sps, freq, buffer_samps, args):
samps = int(sps / args.div)
assert args.chirp_length > 0 and args.chirp_length <= 1.0
csr0 = args.chirp_start * np.pi * 2 / sps
cer0 = args.chirp_end * np.pi * 2 / sps
#csr1 = 80e3 * np.pi * 2 / sps
#cer1 = 100e3 * np.pi * 2 / sps
csamps = int(sps * args.chirp_length)
chirp0 = np.exp(1j * np.add.accumulate(np.linspace(csr0, cer0, csamps)))
#chirp1 = np.exp(1j * np.add.accumulate(np.linspace(csr1, cer1, csamps)))
assert samps % 2 == 0
t = samps / sps
sig0 = np.exp(1j * np.linspace(0, np.pi * 2 * args.local_freq_a * t, samps))
sig1 = np.exp(1j * np.linspace(0, np.pi * 2 * args.local_freq_b * t, samps))
sig2 = np.exp(1j * np.linspace(0, np.pi * 2 * args.local_freq_c * t, samps))
t = samps * 0.5 / sps
#sig0 = np.exp(1j * np.linspace(0, np.pi * 2 * args.local_freq_a * t, int(samps // 2)))
#sig1 = np.exp(1j * np.linspace(0, np.pi * 2 * args.local_freq_b * t, int(samps // 2)))
#sig0 = np.hstack([np.conjugate(sig0[::-1][:-1]), sig0 * -1])
#sig1 = np.hstack([np.conjugate(sig1[::-1]), sig1 * -1])
# create a phase jump where the phase of both signals should be the same
sig2[int(samps // 2):] *= -1.0
#sig1[int(samps // 4):] *= -1.0
#sig1 = np.hstack([sig1[::-1], sig1 * -1])
if args.tx:
# non-chirp signal should stay at about 50% power all the way even
# though the chirp may end sooner; constant power
tx_data0 = sig0 + sig1 + sig2
#tx_data0[0:len(chirp0)] += chirp0
tx_data0 /= np.max(np.abs(tx_data0))
tx_data0 *= 2000
tx_data2 = np.zeros((len(tx_data0) * 4), np.int16)
tx_data2[0::4] = tx_data0.real
tx_data2[1::4] = tx_data0.imag
tx_data2[2::4] = 0
tx_data2[3::4] = 0
tx_data = tx_data2.tobytes() * (args.div * 2)
cards[0].set_tx_data(tx_data)
#cards[0].set_tx_gain(30)
input('Press Enter To Stop')
cards[0].exit()
else:
# Flush the junk from start-up that is in the buffers.
_, sa, sb = cards[0].get_samples(sps)
delta = 2e3
#sig_sos_a = signal.butter(
# 8,
# (args.local_freq_a - delta, args.local_freq_a + delta),
# btype='bandpass',
# output='sos',
# fs=sps
#)
#sig_sos_b = signal.butter(
# 8,
# (args.local_freq_b - delta, args.local_freq_b + delta),
# btype='bandpass',
# output='sos',
# fs=sps
#)
a = args.local_freq_a - delta
b = args.local_freq_a
c = args.local_freq_a + delta
d = args.local_freq_b - delta
e = args.local_freq_b
f = args.local_freq_b + delta
g = args.local_freq_c - delta
h = args.local_freq_c
i = args.local_freq_c + delta
sig_fir_a = signal.firwin2(
128, (0, a, b, c, sps / 2), (0.0, 0.5, 250.0, 0.5, 0.0), fs=sps
)
sig_fir_b = signal.firwin2(
128, (0, d, e, f, sps / 2), (0.0, 0.5, 250.0, 0.5, 0.0), fs=sps
)
sig_fir_c = signal.firwin2(
128, (0, g, h, i, sps / 2), (0.0, 0.5, 250.0, 0.5, 0.0), fs=sps
)
sol = 299792458
fd = open('sa.pickle', 'wb')
j = []
while True:
rx_counter, sa, sb = cards[0].clear_buffer_get_samples(
int(sps / args.div)
)
sam = np.abs(sa)
if not args.just_avg_phase:
print('mean', np.mean(sam), 'peak', np.max(sam))
#cc0 = signal.correlate(sa, chirp0, mode='valid')
#ccm0 = np.abs(cc0)
#ndx0 = np.argmax(ccm0)
#cc1 = signal.correlate(sa, chirp1, mode='valid')
#ccm1 = np.abs(cc1)
#ndx1 = np.argmax(ccm1)
# extract just signal 0 (sinusodial)
#sc0 = signal.sosfiltfilt(sig_sos_a, sa)
# extract just signal 1 (sinusodial)
#sc1 = signal.sosfiltfilt(sig_sos_b, sa)
sc0 = signal.convolve(sa, sig_fir_a, mode='valid')
sc1 = signal.convolve(sa, sig_fir_b, mode='valid')
sc2 = signal.convolve(sa, sig_fir_c, mode='valid')
sg0 = sc0[1:] * np.conjugate(sc0[:-1])
ta0 = np.angle(np.sum(sg0))
ta0_freq = ta0 * sps / (np.pi * 2)
sg1 = sc1[1:] * np.conjugate(sc1[:-1])
ta1 = np.angle(np.sum(sg1))
ta1_freq = ta1 * sps / (np.pi * 2)
sg2 = sc2[1:] * np.conjugate(sc2[:-1])
ta2 = np.angle(np.sum(sg2))
ta2_freq = ta2 * sps / (np.pi * 2)
lock0 = abs(ta0_freq - args.local_freq_a) < 2e3
lock1 = abs(ta1_freq - args.local_freq_b) < 2e3
lock2 = abs(ta2_freq - args.local_freq_c) < 2e3
if not lock0 or not lock1 or not lock2:
print('WARNING: one or more signals not acquired [%s/%s/%s]' % (
lock0, lock1, lock2
))
print('WARNING: check transmitter is running and --local-freq-*')
print(' options are set correctly')
continue
if not args.just_avg_phase:
print('signals A=%.3fkhz B=%.3fkhz C=%.3fkhz' % (ta0_freq / 1e3, ta1_freq / 1e3, ta2_freq / 1e3))
gg = np.abs(np.angle(sg2))
gg = (gg - np.mean(gg)) / np.std(gg)
phase_jump_ndx = np.argmax(gg)
if gg[phase_jump_ndx] < 10:
print('WARNING: weak phase jump; check signal SNR')
continue
aa = sc0[phase_jump_ndx]
bb = sc1[phase_jump_ndx]
cc = aa * np.conjugate(bb)
# bb is ahead in phase (12khz ahead in phase)
if not args.just_avg_phase:
print('phase difference during phase transition', np.angle(cc))
print('phase_jump_ndx', phase_jump_ndx)
j.append(cc)
if not args.just_avg_phase:
print('averaged phase difference', np.angle(np.sum(j)))
else:
print(np.angle(np.sum(j)))
#pickle.dump((sc0, sc1, sg2), fd)
#exit()
def main(args):
if args.tx:
initial_tx_gain = 15
else:
initial_tx_gain = -24
cards, buffer_samps = brfharness.setup([args.serial], args.sps, args.freq, initial_tx_gain)
entry(cards, args.sps, args.freq, buffer_samps, args)
if __name__ == '__main__':
ap = argparse.ArgumentParser()
ap.add_argument('--serial', type=str, required=True)
ap.add_argument('--freq', type=float, required=True)
ap.add_argument('--local-freq-a', type=float, required=True)
ap.add_argument('--local-freq-b', type=float, required=True)
ap.add_argument('--local-freq-c', type=float, required=True)
ap.add_argument('--chirp-start', type=float, required=True)
ap.add_argument('--chirp-end', type=float, required=True)
ap.add_argument('--chirp-length', type=float, required=True)
ap.add_argument('--tx', action=argparse.BooleanOptionalAction, default=False)
ap.add_argument('--sps', type=int, required=True)
ap.add_argument('--div', type=int, default=8)
ap.add_argument('--just-avg-phase', action=argparse.BooleanOptionalAction, default=False)
main(ap.parse_args())But I’ve yet to confirm by moving the board enough times. I’m still testing it to see if I am right.
You can use --just-avg-phase to get a cleaner output that is easier to read as it scrolls.
The --div was added to increase the frequency of measurements. It is one second divided by that integer factor for the time of each measurement. A value of 8 means 1/8th of a second.
Update
I’ve seen some issues with the above method. For one, it isn’t meeting my requirements for what I expected it to do when moving the board around. That is requiring me to take a closer look at what is going wrong and why. I’ve also got some thinking to do over the phase reversal itself because I feel like it could be possible for it to change location based on propagation also.
I hope to continue working on this project, but I also hope it provides someone else with the foundation to investigate phase themselves. You should be able to run the programs and examine the mathematical relationships to find your own insight into the world of radio and if that is the case then this page has accomplished its goal.
Update
I think I’ve finally figured out the root reason why the experiment doesn’t work. I was thinking about the wave from the perspective of after the mixer. The real issue is that per sample at the frequencies I’m working with many cycles of the actual wave happen per sample and the number of cycles per sample isn’t an integer meaning the phase at which the wave is sampled after the mixer is not going to be the same phase the next time I sample because the wave is likely either slowly falling behind or moving forward from the view of the sample.
For example, even though I create a phase transition at a specific sample, and I find this phase transition at the receiver at a specific RX sample the actual point along the real wave that is being sampled isn’t going to be in the same place each time. This is because the wave itself was off.
If I have a frequency of 200e6 with a sampling rate of 520834 samples per second this means the physical wave rotates in phase ~383.9995084 times per sample. If I were to sample this the first time and it had a phase of X and the clock was perfectly stable, then the next sample would be at phase (radians) X + ~6.280 and the next at (radians) X + ~6.277. I can come to this conclusion with the equation (freq / sps * np.pi * 2 * sample_index) % (np.pi * 2) which shows that each time I sample the wave its phase isn’t going to be the same.
It would seem possible to select a frequency that did produce an integer number of cycles per sampling period; however, this might not be practical due to the precision of the frequency tuner, LO stability, the sampling clock stability, and likely some other issues. Would it help though?
Furthermore, even the phase transition detection method suffers from this problem because each phase transition sample point measured the wave at a slightly different phase point since it would too be governed by the above equation.
It seems possible to compensate but the issue of how stable the sampling clock is would be a big factor. I will have to try to compensate and see if that produces any viable results.
A Different Try
I was thinking on my assumptions from earlier. I realized that I needed the LO (local oscillator) wave to reverse the mixer process and produce the actual phase of the measured wave at the sample points. I’m ignoring all the noise at this point and just considering the ideal case.
The ideal case is the physical wave arrived at the mixer. The equivalent operation was physical_wave_signal * np.conjugate(mixer_lo_signal) which produced the output that was sampled by the ADC. So, if I had the mixer_lo_signal or the equivalent then I could reverse the process. Even better I would seem to only need the mixer_lo_signal at the same sampling rate and number of samples.
If I did have the mixer_lo_signal I could just do mixer_output_adc_sampled * mixer_lo_signal and get measures of the physical wave at the time it was sampled if the above was discrete samples.
Now, since I only want to consider a single sample taken during the phase transition I wouldn’t need to do every sample. From this point, consider that I took twenty measurements which means I took one measurement for every phase transition.
Since we don’t know the exact LO (local oscillator) and on top of that we could assume that our LO isn’t perfectly stable nor is our ADC sampling clock we could imagine our samples are not uniform due to the ADC sampling clock instability.
At this point, we have two vectors of twenty samples. One vector, va, is for --local-freq-a and the other, vb, is for --local-freq-b. It would seem that there would be another vector, lv, representing the LO samples such that:
np.sqrt(np.std(np.angle(va * lv)) ** 2 + np.std(np.angle(vb * lv)) ** 2)This would be some lv that would minimize the output of the equation and this lv would represent the approximated LO sample points. I’m not sure if I should have just added the standard deviations instead but I think I’ve articulated the idea at the least.
In other words, some lv would produce va angles that were all close to one another and the same for vb.
This is if I ignore the non-uniform sampling nature of the ADC since it likely had some clock jitter but perhaps that clock jitter would also be represented in lv since we no longer have to consider either vector as a sequence of uniform samples.
Here is the code to try to find this lv vector in Python. It also writes out a file called work.bin that can be used by the Rust-lang program further below. Rust is quite a bit quicker than Python with tight loops.
import argparse
import brfharness
import argparse
import numpy as np
import scipy.signal as signal
import struct
import queue
import threading
import time
import pickle
def entry(cards, sps, freq, buffer_samps, args):
samps = int(sps / args.div)
assert args.chirp_length > 0 and args.chirp_length <= 1.0
csr0 = args.chirp_start * np.pi * 2 / sps
cer0 = args.chirp_end * np.pi * 2 / sps
#csr1 = 80e3 * np.pi * 2 / sps
#cer1 = 100e3 * np.pi * 2 / sps
csamps = int(sps * args.chirp_length)
chirp0 = np.exp(1j * np.add.accumulate(np.linspace(csr0, cer0, csamps)))
#chirp1 = np.exp(1j * np.add.accumulate(np.linspace(csr1, cer1, csamps)))
assert samps % 2 == 0
t = samps / sps
sig0f = np.exp(1j * np.linspace(0, np.pi * 2 * args.local_freq_a * t, samps))
sig1f = np.exp(1j * np.linspace(0, np.pi * 2 * args.local_freq_b * t, samps))
sig2f = np.exp(1j * np.linspace(0, np.pi * 2 * args.local_freq_c * t, samps))
tail = int(samps // 4)
print('tail was %d' % tail)
sig0 = sig0f.copy()
sig1 = sig1f.copy()
sig2 = sig2f.copy()
# taper the beginning and ends to stop splattering
sig0[:tail] *= np.linspace(0.0, 1.0, tail)
sig0[:tail] *= np.linspace(0.0, 1.0, tail)
sig0[:tail] *= np.linspace(0.0, 1.0, tail)
sig0[-tail:] *= np.linspace(1.0, 0.0, tail)
sig1[-tail:] *= np.linspace(1.0, 0.0, tail)
sig2[-tail:] *= np.linspace(1.0, 0.0, tail)
t = samps * 0.5 / sps
#sig0 = np.exp(1j * np.linspace(0, np.pi * 2 * args.local_freq_a * t, int(samps // 2)))
#sig1 = np.exp(1j * np.linspace(0, np.pi * 2 * args.local_freq_b * t, int(samps // 2)))
#sig0 = np.hstack([np.conjugate(sig0[::-1][:-1]), sig0 * -1])
#sig1 = np.hstack([np.conjugate(sig1[::-1]), sig1 * -1])
# create a phase jump where the phase of both signals should be the same
sig2[int(samps // 2):] *= -1.0
#sig1[int(samps // 4):] *= -1.0
#sig1 = np.hstack([sig1[::-1], sig1 * -1])
if args.tx:
# non-chirp signal should stay at about 50% power all the way even
# though the chirp may end sooner; constant power
tx_data0 = sig0 + sig1 + sig2
#tx_data0[0:len(chirp0)] += chirp0
tx_data0 /= np.max(np.abs(tx_data0))
tx_data0 *= 2000
tx_data2 = np.zeros((len(tx_data0) * 4), np.int16)
tx_data2[0::4] = tx_data0.real
tx_data2[1::4] = tx_data0.imag
tx_data2[2::4] = 0
tx_data2[3::4] = 0
tx_data = tx_data2.tobytes() * (args.div * 2)
cards[0].set_tx_data(tx_data)
#cards[0].set_tx_gain(30)
input('Press Enter To Stop')
cards[0].exit()
else:
# Flush the junk from start-up that is in the buffers.
_, sa, sb = cards[0].get_samples(sps)
delta = 2e3
#sig_sos_a = signal.butter(
# 8,
# (args.local_freq_a - delta, args.local_freq_a + delta),
# btype='bandpass',
# output='sos',
# fs=sps
#)
#sig_sos_b = signal.butter(
# 8,
# (args.local_freq_b - delta, args.local_freq_b + delta),
# btype='bandpass',
# output='sos',
# fs=sps
#)
a = args.local_freq_a - delta
b = args.local_freq_a
c = args.local_freq_a + delta
d = args.local_freq_b - delta
e = args.local_freq_b
f = args.local_freq_b + delta
g = args.local_freq_c - delta
h = args.local_freq_c
i = args.local_freq_c + delta
sig_fir_a = signal.firwin2(
128, (0, a, b, c, sps / 2), (0.0, 0.5, 250.0, 0.5, 0.0), fs=sps
)
sig_fir_b = signal.firwin2(
128, (0, d, e, f, sps / 2), (0.0, 0.5, 250.0, 0.5, 0.0), fs=sps
)
sig_fir_c = signal.firwin2(
128, (0, g, h, i, sps / 2), (0.0, 0.5, 250.0, 0.5, 0.0), fs=sps
)
sol = 299792458
print('loading')
m = []
for x in range(20):
sc = int(sps / args.div)
if cards[0].rx_rx.qsize() < 10:
while cards[0].rx_tx.qsize() < 10:
cards[0].rx_tx.put(('request', sc))
rx_counter, sa, _ = cards[0].rx_rx.get()
sc0 = signal.convolve(sa, sig_fir_a, mode='valid')
sc1 = signal.convolve(sa, sig_fir_b, mode='valid')
sc2 = signal.convolve(sa, sig_fir_c, mode='valid')
sg0 = sc0[1:] * np.conjugate(sc0[:-1])
ta0 = np.angle(np.sum(sg0))
ta0_freq = ta0 * sps / (np.pi * 2)
sg1 = sc1[1:] * np.conjugate(sc1[:-1])
ta1 = np.angle(np.sum(sg1))
ta1_freq = ta1 * sps / (np.pi * 2)
sg2 = sc2[1:] * np.conjugate(sc2[:-1])
ta2 = np.angle(np.sum(sg2))
ta2_freq = ta2 * sps / (np.pi * 2)
lock0 = abs(ta0_freq - args.local_freq_a) < 2e3
lock1 = abs(ta1_freq - args.local_freq_b) < 2e3
lock2 = abs(ta2_freq - args.local_freq_c) < 2e3
if not lock0 or not lock1 or not lock2:
print('WARNING: one or more signals not acquired [%s/%s/%s]' % (
lock0, lock1, lock2
))
print('WARNING: check transmitter is running and --local-freq-*')
print(' options are set correctly')
continue
gg = np.abs(np.angle(sg2))
gg = (gg - np.mean(gg)) / np.std(gg)
phase_jump_ndx = np.argmax(gg)
if gg[phase_jump_ndx] < 10:
print('WARNING: weak phase jump; check signal SNR')
continue
m.append((sc0[phase_jump_ndx], sc1[phase_jump_ndx]))
m = np.array(m)
m = np.swapaxes(m, 0, 1)
# Write the data to be run in Rust-lang for computation.
fd = open('work.bin', 'wb')
fd.write(struct.pack('<I', m.shape[1]))
for x in range(m.shape[1]):
fd.write(struct.pack('<dd', m[0, x].real, m[0, x].imag))
for x in range(m.shape[1]):
fd.write(struct.pack('<dd', m[1, x].real, m[1, x].imag))
fd.flush()
fd.close()
best_std = None
print('processing')
while True:
# consider non-uniform sampling
# estimate the LO non-uniform points
h = np.exp(1j * ((np.random.random(m.shape[1]) * 2 - 1) * np.pi))
mh = m * h
mha = np.angle(mh)
std = np.std(mha)
if best_std is None or std < best_std:
mhs = np.sum(mh, axis=1)
fa = np.angle(mhs[0] * np.conjugate(mhs[1]))
best_std = std
print(fa, std)
def main(args):
if args.tx:
initial_tx_gain = 25
else:
initial_tx_gain = -24
cards, buffer_samps = brfharness.setup([args.serial], args.sps, args.freq, initial_tx_gain)
entry(cards, args.sps, args.freq, buffer_samps, args)
if __name__ == '__main__':
ap = argparse.ArgumentParser()
ap.add_argument('--serial', type=str, required=True)
ap.add_argument('--freq', type=float, required=True)
ap.add_argument('--local-freq-a', type=float, required=True)
ap.add_argument('--local-freq-b', type=float, required=True)
ap.add_argument('--local-freq-c', type=float, required=True)
ap.add_argument('--chirp-start', type=float, required=True)
ap.add_argument('--chirp-end', type=float, required=True)
ap.add_argument('--chirp-length', type=float, required=True)
ap.add_argument('--tx', action=argparse.BooleanOptionalAction, default=False)
ap.add_argument('--sps', type=int, required=True)
ap.add_argument('--div', type=int, default=8)
ap.add_argument('--just-avg-phase', action=argparse.BooleanOptionalAction, default=False)
main(ap.parse_args())I used a different method to calculate the score of the solution in Rust. I thought it might handle the angles better than using the standard deviation method.
use byteorder::{LittleEndian, ReadBytesExt};
use std::fs::File;
use std::io::{Cursor, Read};
use std::vec::Vec;
use num::complex::Complex;
use rand::prelude::*;
use statistical::standard_deviation;
fn angle_distances2(v: &Vec<Complex<f64>>) -> f64 {
let mut total_distance = 0.0f64;
for x in 0..v.len() - 1 {
total_distance += f64::abs((v[x] * v[x+1].conj()).arg());
}
total_distance
}
fn angle_distances(v: &Vec<Complex<f64>>) -> f64 {
let mut total_distance = 0.0f64;
let mut x = 0usize;
for a in v.iter() {
for b in v[x+1..v.len()].iter() {
total_distance += f64::abs(((*a) * (*b).conj()).arg());
}
x += 1;
}
/*
for x in 0..v.len() {
for y in x + 1..v.len() {
let a = &v[x];
let b = &v[y];
total_distance += f64::abs((a * b.conj()).arg());
}
}
*/
total_distance
}
fn main() {
let mut f = File::open("z:\\test_bench\\work.bin").unwrap();
let mut hdr_buffer = vec![0_u8; 4];
f.read(&mut hdr_buffer).unwrap();
let mut hdr_rdr = Cursor::new(hdr_buffer);
let mut cnt = hdr_rdr.read_u32::<LittleEndian>().unwrap() as usize;
println!("cnt:{cnt}");
let mut v0_buffer = vec![0_u8; cnt * 8 * 2];
let mut v1_buffer = vec![0_u8; cnt * 8 * 2];
f.read(&mut v0_buffer).unwrap();
f.read(&mut v1_buffer).unwrap();
let mut v0_rdr = Cursor::new(v0_buffer);
let mut v1_rdr = Cursor::new(v1_buffer);
let mut v0 = vec![Complex { re: 0.0f64, im: 0.0f64 }; cnt];
let mut v1 = vec![Complex { re: 0.0f64, im: 0.0f64 }; cnt];
for x in 0..cnt {
let v0_real = v0_rdr.read_f64::<LittleEndian>().unwrap();
let v0_imag = v0_rdr.read_f64::<LittleEndian>().unwrap();
let v1_real = v1_rdr.read_f64::<LittleEndian>().unwrap();
let v1_imag = v1_rdr.read_f64::<LittleEndian>().unwrap();
v0[x] = Complex::new(v0_real, v0_imag);
v1[x] = Complex::new(v1_real, v1_imag);
}
let mut rng = rand::thread_rng();
let mut h = vec![Complex { re: 0.0f64, im: 0.0f64 }; cnt];
let mut nv0 = vec![Complex { re: 0.0f64, im: 0.0f64 }; cnt];
let mut nv1 = vec![Complex { re: 0.0f64, im: 0.0f64 }; cnt];
let mut a0 = vec![0_f64; cnt];
let mut a1 = vec![0_f64; cnt];
let mut best_std: Option<f64> = None;
loop {
for it in h.iter_mut().zip(v0.iter()).zip(v1.iter()).zip(nv0.iter_mut()).zip(nv1.iter_mut()) {
let ((((hi, v0i), v1i), nv0i), nv1i) = it;
let theta = (rng.gen::<f64>() * 2.0 - 1.0) * std::f64::consts::PI;
hi.re = f64::cos(theta);
hi.im = f64::sin(theta);
*nv0i = *v0i * *hi;
*nv1i = *v1i * *hi;
}
/*
for x in 0..cnt {
let theta = (rng.gen::<f64>() * 2.0 - 1.0) * std::f64::consts::PI;
h[x].re = f64::cos(theta);
h[x].im = f64::sin(theta);
}
for x in 0..cnt {
nv0[x] = v0[x] * h[x];
nv1[x] = v1[x] * h[x];
//a0[x] = (v0[x] * h[x]).arg();
//a1[x] = (v1[x] * h[x]).arg();
}
*/
//let std0 = standard_deviation(&a0, None);
//let std1 = standard_deviation(&a1, None);
//let std = f64::sqrt(std0 * std0 + std1 * std1);
let std0 = angle_distances2(&nv0);
let std1 = angle_distances2(&nv1);
let std = std0 + std1;
best_std = match best_std {
None => Some(std),
Some(v) => if std < v {
println!("{std} {std0} {std1}");
let mut nv0avg = Complex { re: 0.0f64, im: 0.0f64 };
let mut nv1avg = Complex { re: 0.0f64, im: 0.0f64 };
for x in 0..nv0.len() {
nv0avg += nv0[x];
let theta = nv0[x].arg() / std::f64::consts::PI * 180.0;
print!("{theta:.1} ");
}
let avg0_theta = nv0avg.arg() / std::f64::consts::PI * 180.0;
println!("\navg: {avg0_theta:.3}");
for x in 0..nv1.len() {
nv1avg += nv1[x];
let theta = nv1[x].arg() / std::f64::consts::PI * 180.0;
print!("{theta:.1} ");
}
let avg1_theta = nv1avg.arg() / std::f64::consts::PI * 180.0;
println!("\navg: {avg1_theta:.3}");
let delta = (nv0avg * nv1avg.conj()).arg() / std::f64::consts::PI * 180.0;
println!("delta: {delta:.3}");
Some(std)
} else {
Some(v)
},
};
}
}
Unfortunately, I couldn’t find a really good solution in a decent amount of time. The problem might lend itself to a gradient descent. I did not check to see if the solution space has a gradient that can be descended. In hindsight, a 20 element solution space is quite vast so perhaps there is a solution it is just hard to find.