I’ve spent years lightly studying electronics. I finally sat down and started working through some formal material. One of the things that has always given me a lot of trouble was understanding the maximum power transfer theorem. I feel stupid about it because it turns out to be very simple. For some reason, over the years I just never really sat down and did the calculations.
It turns out things are more complicated than they seem. I always wondered why the source impedance had to match the load impedance to transfer the maximum amount of power to the load.
It really turns out that a very simple graph of what is happening can reveal the hidden world of what is going on.
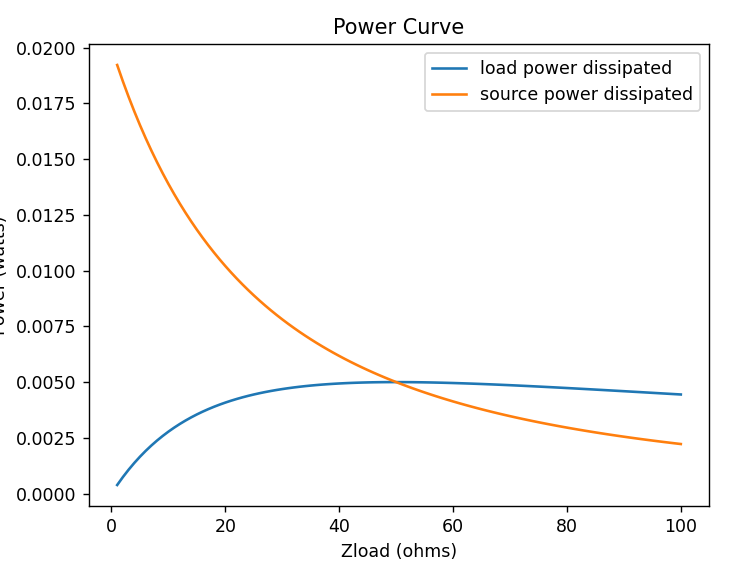
Take for instance a circuit with a voltage source and two resistors or impedances in series. I’m going to use resistance because impedance requires the complex conjugate to be in place which complicates things just a bit.
Let us say this circuit’s voltage source is one volt and the first resistor which is part of the source circuit is 50-ohm. Now, to create the chart you simply alter the second resistor, the load, from 1-ohm to 100-ohms and that creates the blue line.
Let me work through the equation: I = V / (R0 + R1). Here we have the current being calculated from the voltage and both resistances. Next, calculate the power dissipated in one of the resistors using I^2 * R1 and in this case with R1 I’m using the load resistor.
The orange line is the source resistance in the graph. You can see how it slowly dissipates less power as you increase the load resistance. If you ask me this shows how you could make the source circuit hotter by not matching the correct load because you cause it to dissipate more heat. The point where they meet just so happens to be when the load resistance equals the source resistance and in the graph above that is at 50-ohms.
Another take away from this graph, is the fact that it appears it would be better to have a higher load resistance than a lower one. You can see the drop off is more steep when the load resistance is less than the source resistance.
Now, I’ve also been working with impedances and AC sources. It turns out the whole thing works almost the same for impedances except you’re load has to cancel out the reactance of the source – the reason for the complex conjugate.
If you have not worked with impedances the idea of the complex conjugate is likely confusing. It deals with a complex number and how the imaginary axis represents the reactance of the circuit – capacitive or inductive.
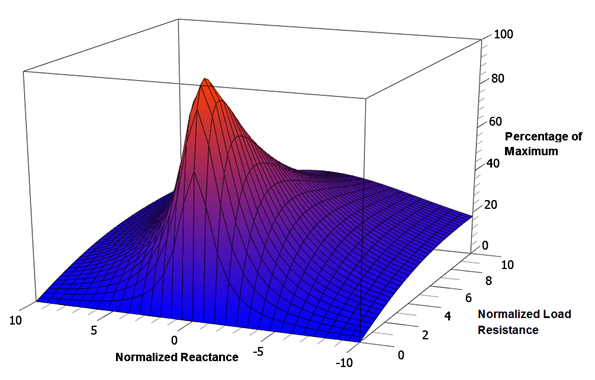
I found the above image from the URL, 5.5: Maximum Power Transfer Theorem – Engineering LibreTexts, which is where I’ve been learning about the theorem. I’ve found it to be a great online resource.
The above graph is very interesting because it does the same thing as my graph except it considers reactance. The normalized reactance shows how not having the reactance cancel out causes less power to be dissipated in the load. This is part of the complexity of using impedances.
I shouldn’t call it complex as if it is impossible or difficult. I just use the word to reference the idea that there are additional factors to be considered when dealing with impedances.
Who would have known such a mysterious phenomenon has such a simple reason?