This test consists of a loopback cable through a 30dB attenuator with the cable being switched between ports. The output is the maximum absolute magnitude of any sample. The SWA and SWB are the configured ports in software of which the available selections are: 0, 1, 2, 3. The SWAGAIN and SWBGAIN are the gain values assigned to each port of SWA and SWB. The HWP is the hardware ports the loopback cable is connected between.
| SWA | SWAGAIN | SWB | SWBGAIN | HWP | HWP | OUTPUT |
| 0 | 60 | 1 | -23 | RX1 | TX1 | 31 |
| 0 | 60 | 1 | -23 | RX2 | TX1 | 32 |
| 0 | 60 | 1 | -23 | TX2 | TX2 | 32 |
| 0 | 60 | 1 | -23 | RX1 | TX2 | 31 |
| 0 | 60 | 1 | 0 | RX1 | TX1 | 32 |
| 0 | 60 | 1 | 0 | RX2 | TX1 | 35 |
| 0 | 60 | 1 | 0 | RX2 | TX2 | 35 |
| 0 | 60 | 1 | 0 | RX1 | TX2 | 32 |
| 0 | 60 | 3 | 0 | RX1 | TX2 | 32 |
| 0 | 60 | 3 | 30 | RX1 | TX2 | 167 |
| 0 | 60 | 3 | 30 | RX2 | TX2 | 50 |
| 0 | 60 | 3 | 30 | RX2 | TX1 | 45 |
| 0 | 60 | 3 | 30 | RX1 | TX1 | 51 |
| 0 | 60 | 1 | 30 | RX1 | TX1 | 164 |
I did not mention that there is a 30dB attenuator on the loopback cable.
From the above data, it should be seen that the following is true. The SPA and SPB is software port A and B. The HPA and HPB is hardware port A and B.
| SPA | SPB | HPA | HPB |
| 0 | 1 | RX1 | TX1 |
| 0 | 3 | RX1 | TX2 |
This proves that the testing is indeed using RX1 and TX2. It partly shows that the amplifiers are functioning for which I’m sure they likely are fine.
Unfortunately, testing is still showing the same reflection pattern even when using a more omni-directional receive antenna. I’ve turned the TX gain down to zero and appending this data to the end of the data with the TX gain set to 60 to verify that indeed the pattern is created by the transmitting antenna.
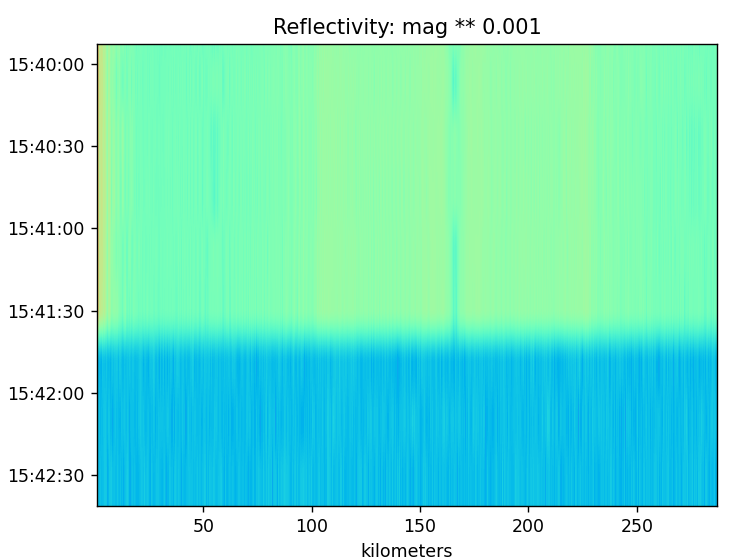
For which the above plot shows that indeed once the transmitting antenna is decreased in power it becomes visible as the light blue region near the bottom. It is apparent the transmitting antenna is creating the pattern. The question is how is the pattern created?
It is possible I could be clipping the RX with too strong of a TX signal. The entire chirp is currently 10-second long which is far longer than the time period being displayed above. If the TX is overdriving the RX it would seem possible for it to create some of the features seen?
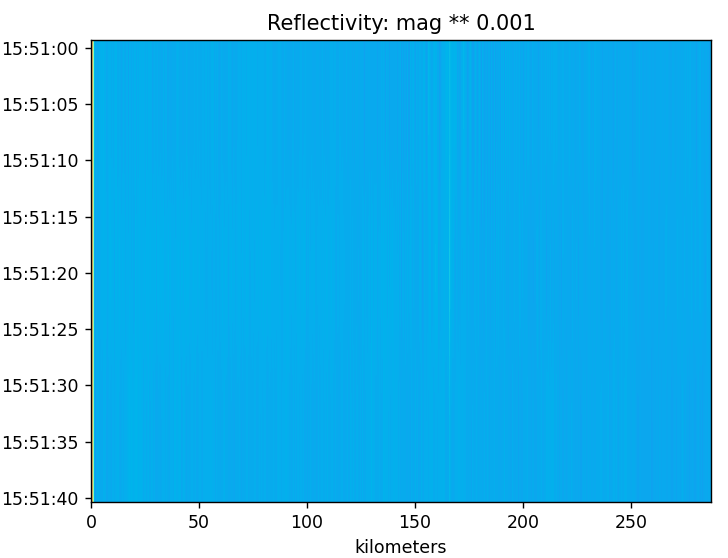
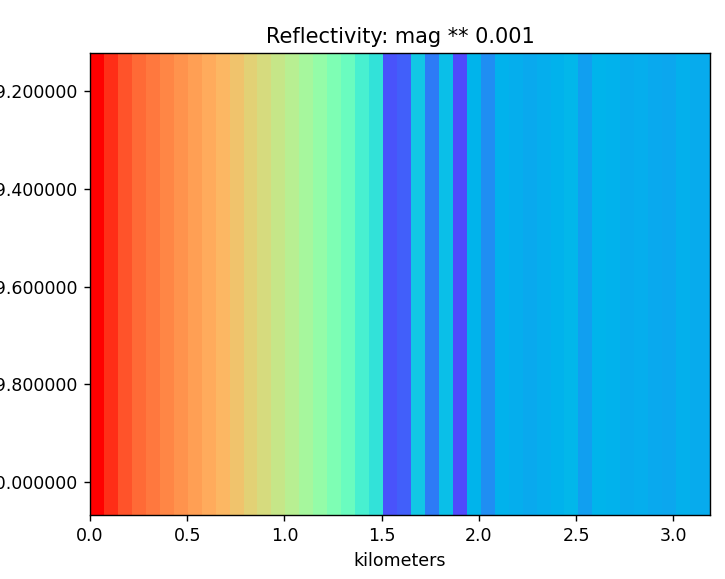
With 40dB of transmit power the above is plotted. The big patterns in the hundreds of kilometers are gone. there is mostly just the simple gradient of correlation magnitude decreasing from 0km to 1.5km. A few gaps after 1.5km.
I am tempted to say perhaps my problem was driving too much power on TX and that was corrupting the RX signal from clipping and such forth. I’ve also realized now that I’ve got a problem to contend with. From what I read most radars have a very brief transmit window and along receive window but what I’ve done to increase power is create a very long duration transmit window which completely swamps the RX window meaning I can’t transmit with too much power.
It might be possible for me to locate the RX antenna further away physically and perhaps that way at least the near field won’t cross over as much if any. I would just need to have some decent synchronization between boards or use a fairly long SMA cable to do the testing. I might use a long SMA cable I have and see if that helps.
I did find a very interesting phase pattern.
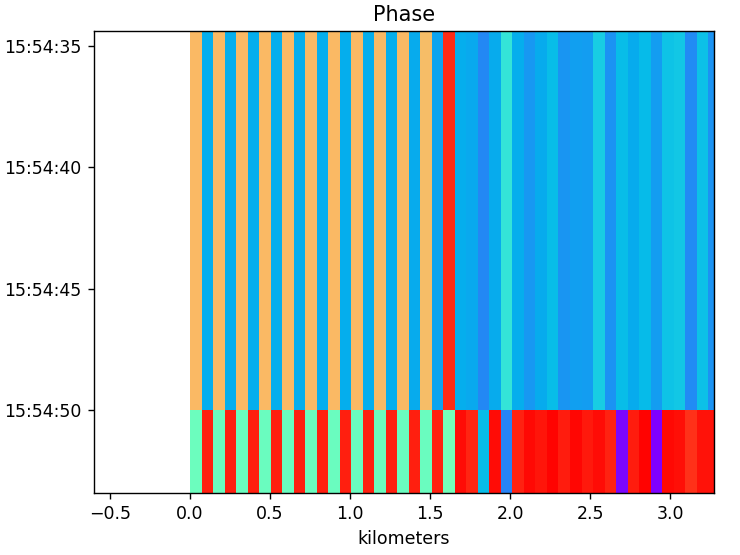
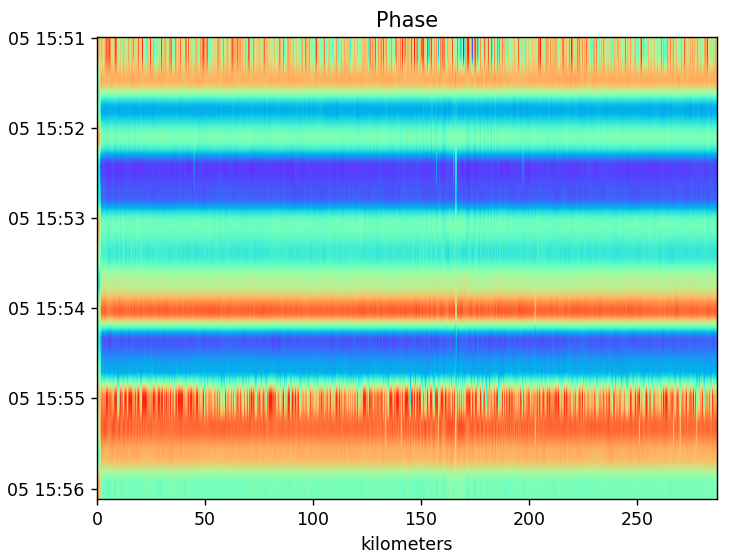
The phase is still starting from some arbitrary offset because that offset seems to dictate the overall coloring of each measurement/scan row. But even more interesting is how the phase is alternating up to roughly 1.5km. It is jumping back and forth.
Each row is jumping by the same amount but sometimes in opposite directions. The amount of about -2.41 radians but sometimes it is 2.25 radians or somewhere around those figures.
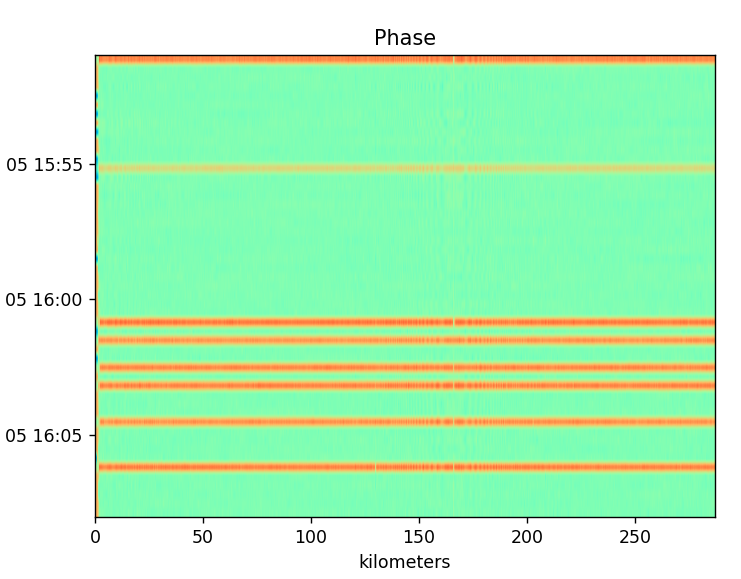
Interesting is when I take the mean of the phase in radians of each row then create the conjugate of that angle as a phase vector and rotate all vectors of that row by that amount. Effectively trying to rotate the entire row to angle zero. This yields output of near constant value showing my assumption was correct that each was starting from some arbitrary phase but showing the same data.
I can’t quite explain the few rows that didn’t turn greenish.
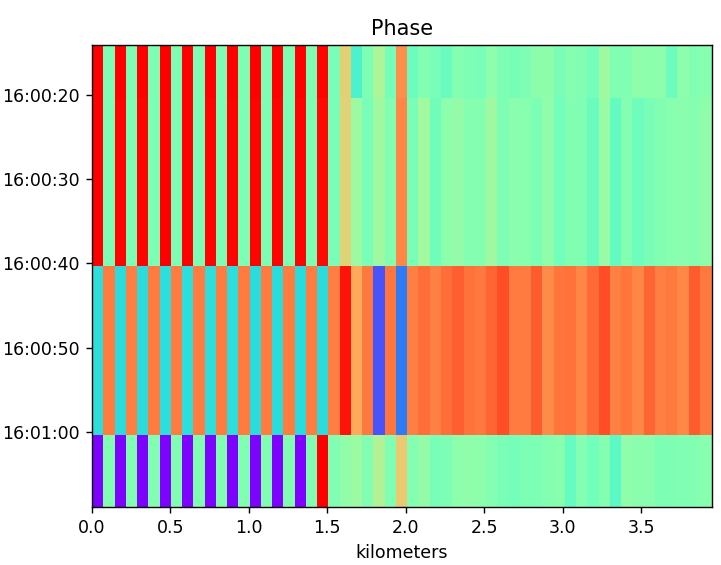
A better transform is to take the phase delta between successive samples. This turns most of the plot greenish.
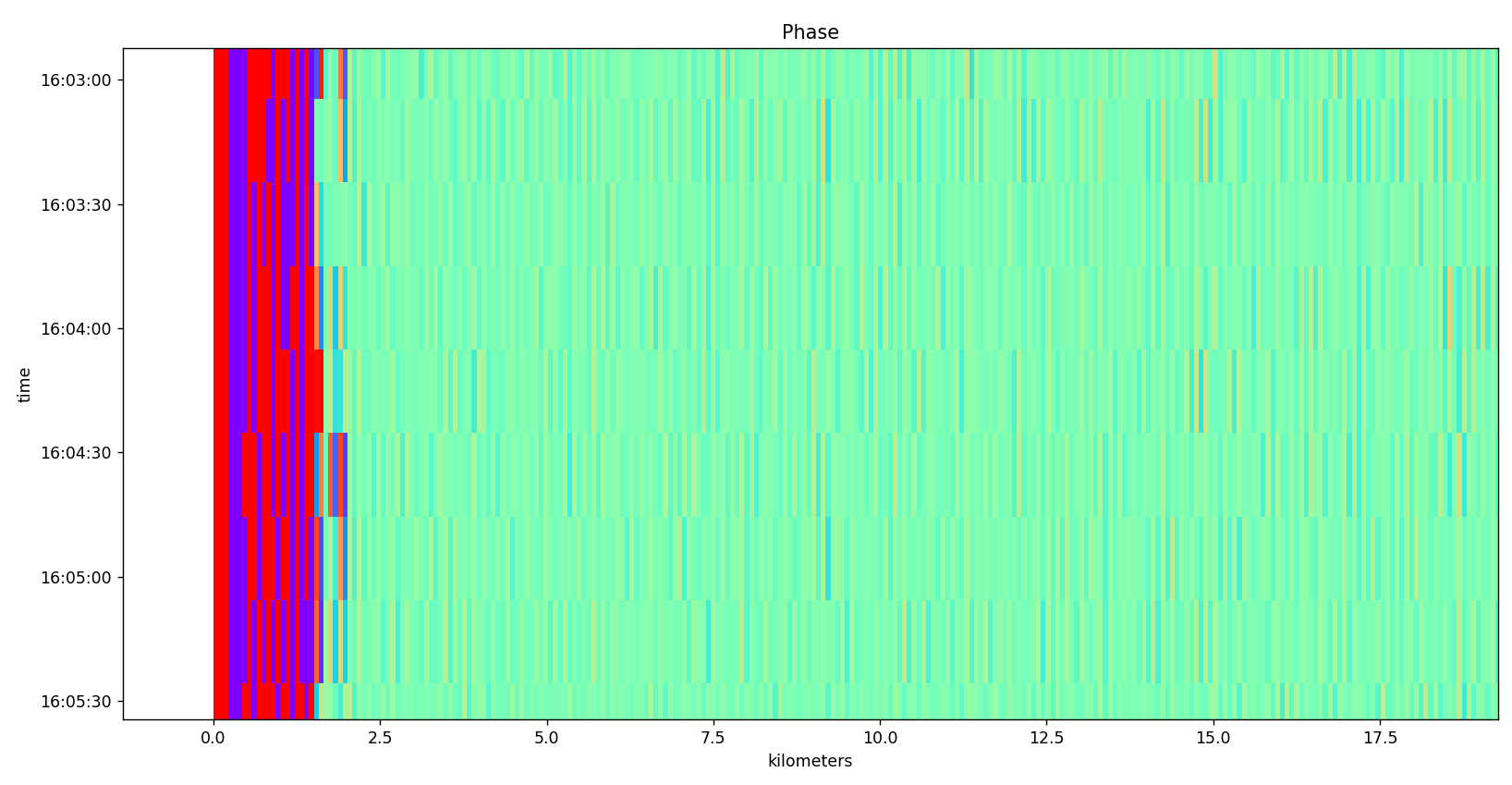
Red are positive phase jumps of about 3.14 and purple are negative phase jumps of about -3.14. It seems my calculations earlier may have been off as this shows the phase jumping 180-degree and not less.
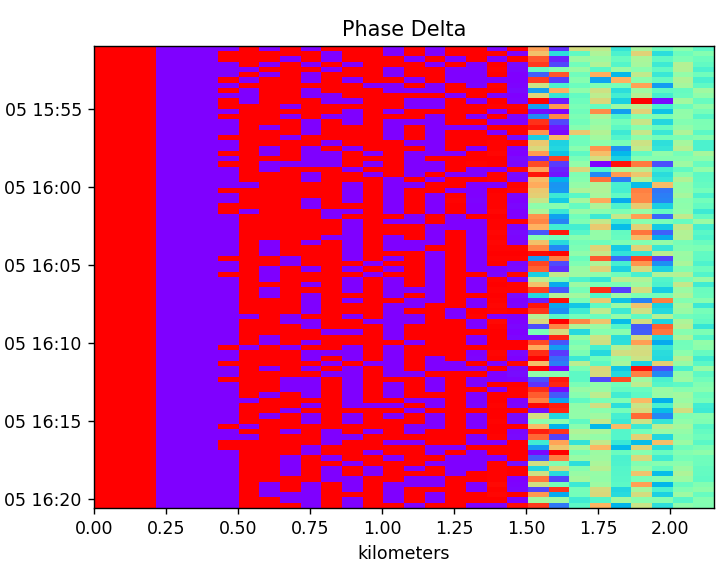
I like this output. It has some consistency. It is realistic in that it seems like the signal falls into the undetectable range around 1.5km. I call that realistic because 10mW shouldn’t go too far. I’m not seeing those weird patterns present far into the hundreds of kilometers once I decreased the TX power. This plot also explains why I’m not seeing changes with the weather. This is because with this kind of range I’m barely if at all seeing the bottom of the clouds.
There are three regions here. The first is from 0km to about 0.24km and it shows a positive phase inversion. The second region is from 0.24km to 0.5km and it shows a negative phase inversion. The third is from 0.5km to about 1.5km and it shows the signal jumping erratically.
Now, -3.14 and +3.14 are basically the same. It doesn’t take much to make it flip between the two extremes. With that in mind I might just consider the bright red and purple the same color. Using that thinking I’m seeing a phase inversion all the way to around 1.5km and then I’m not seeing any phase inversion. This might be in line with the signal encountering higher electrical impedance as it travels until finally it is undetectable.
I also included a peak measurement on the RX baseband stream. With the TX gain set to 30db I’m seeing around 480 as a magnitude and that is out of a scale of around 2894.89 since each I/Q channel can be up to 2047 in value you do sqrt(2047 ** 2 + 2047 ** 2).
I’ve now changed the TX gain from 30dB to 50dB and I’m getting a peak measurement of 1560. Yet, I’m not seeing much distance increase. It still seems to fade out around 1.5km. Is it possible something is at 1.5km like cloud cover and that is eating the signal up? It just seems going from 30dB to 50dB would increase the signal magnitude by 6 times.
Let me try decreasing the TX power and see if that results in decreased distance. I have to establish a relationship with TX power and distance else what I’m seeing may not be correct.
| TX Power | Phase Delta Distance | b0_max |
| 50dB | 1.500km | |
| 30dB | 1.500km | |
| 10dB | 1.400km | |
| 0dB | 1.250km | 34 |
| -10dB | 1.000km | 34 |
The above shows correlation between phase delta distance (an approximation) and TX power used. This is good news. It means that TX power has control over the distance as expected. The b0_max value is the peak magnitude of any sample in the baseband stream. Of note, at about 34 the signal has gone below the noise floor but since I’m using an extremely long correlation, of about 10 seconds, I’m guessing the SNR can go negative which is why I still get results.
I’ve created what I’m going to call a phase delta limit (PDL) test. It does what I was doing by hand except it does it in an automated way. I’ve changed the duration of the chirp in this first run and this is the output so far of the test.
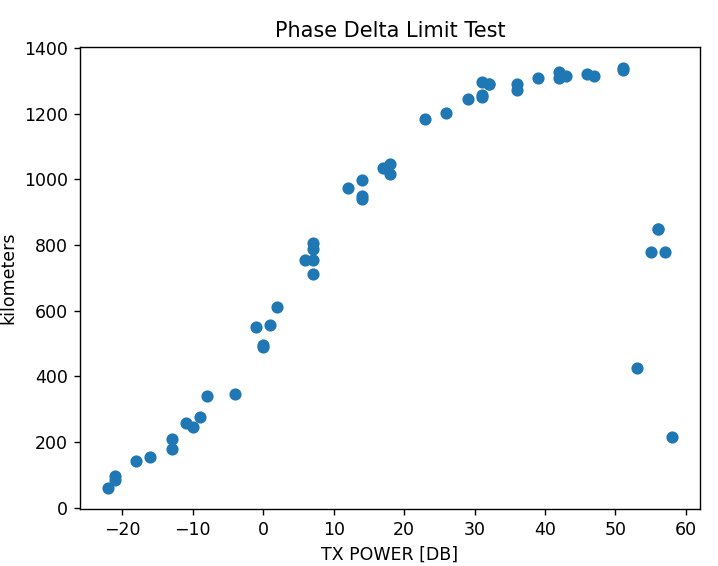
You can see the distance increasing as a function of TX power but at about 51dB there is a sharp and erratic drop off. I think this is the point at which clipping is happening in the RX stream. Where the TX is being driven too hard and causing corruption – those weird patterns at high altitude.
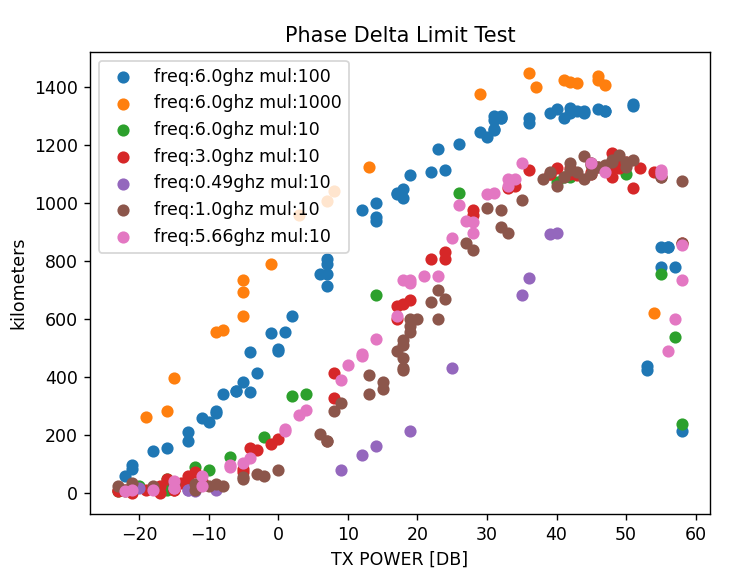
This is a run across various chirp durations, samp_mul, and frequencies. It establishes that distance is a function of frequency and chirp duration. If the test is truly in proportion to some degree with actual distance. I’m basing this all on the assumption that a near 180-degree phase reversal indicates a valid radar return and it might even be possible to get returns that don’t have a full phase reversal? I am not sure of the answer to that.
I’m surprised using a longer duration chirp had so little impact. The CPU and memory cost is very significant especially at higher sampling rates. I was hoping to inch out some decent distance using that method. I’m thinking I’m going to investigate if perhaps I can get decent reflections beyond the PDL test distance.
Back to Reflections
So, I’ve got a better idea about my power level. Now, I just need to figure out exactly how far my reflections are coming from and how to reach out there further if needed. I’m quite sure I’m going about one mile (1.6km) and I’m just not sure if I’m going further. I’ve figured out increasing the chirp duration may or may not have the desired effect.
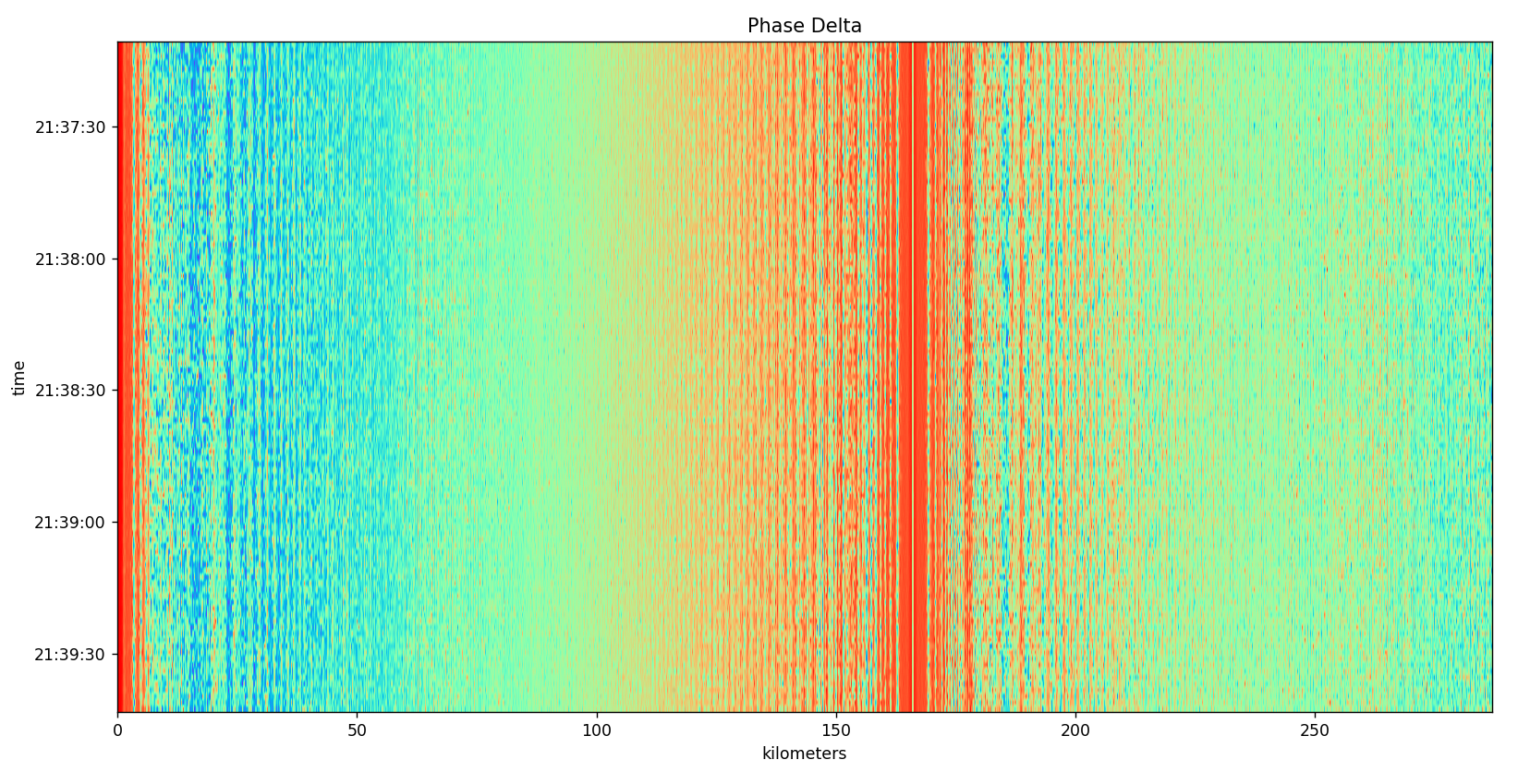
I’ve used the following parameters. The frequency is 5660e6, –samps-mul=10, –tx-gain=48, and samps_factor=0.001. This makes a chirp duration of 0.01 seconds with a linear chirp repeated 10 (–samps-mul) times.
Okay, so once again, I’m struck with this really significant, what should be, reflection at around 166km. It extends far to the left and right. I don’t know what that is. I’d expect to see some atmospheric disturbance under 15km from clouds, humidity, or something. I can see some phase inversions happening in that region and then of course some banding happening at 19km to 40km. Another thing is the big band around 166km is not symmetrical.
I’m just having trouble believing the signal is going that far without hitting some clouds and producing a change over time with the weather. I will just simply have to watch it. Perhaps, the reflection from the water vapor is very minute and hard to see and I might need to subtract out what I am currently seeing in order to see that.
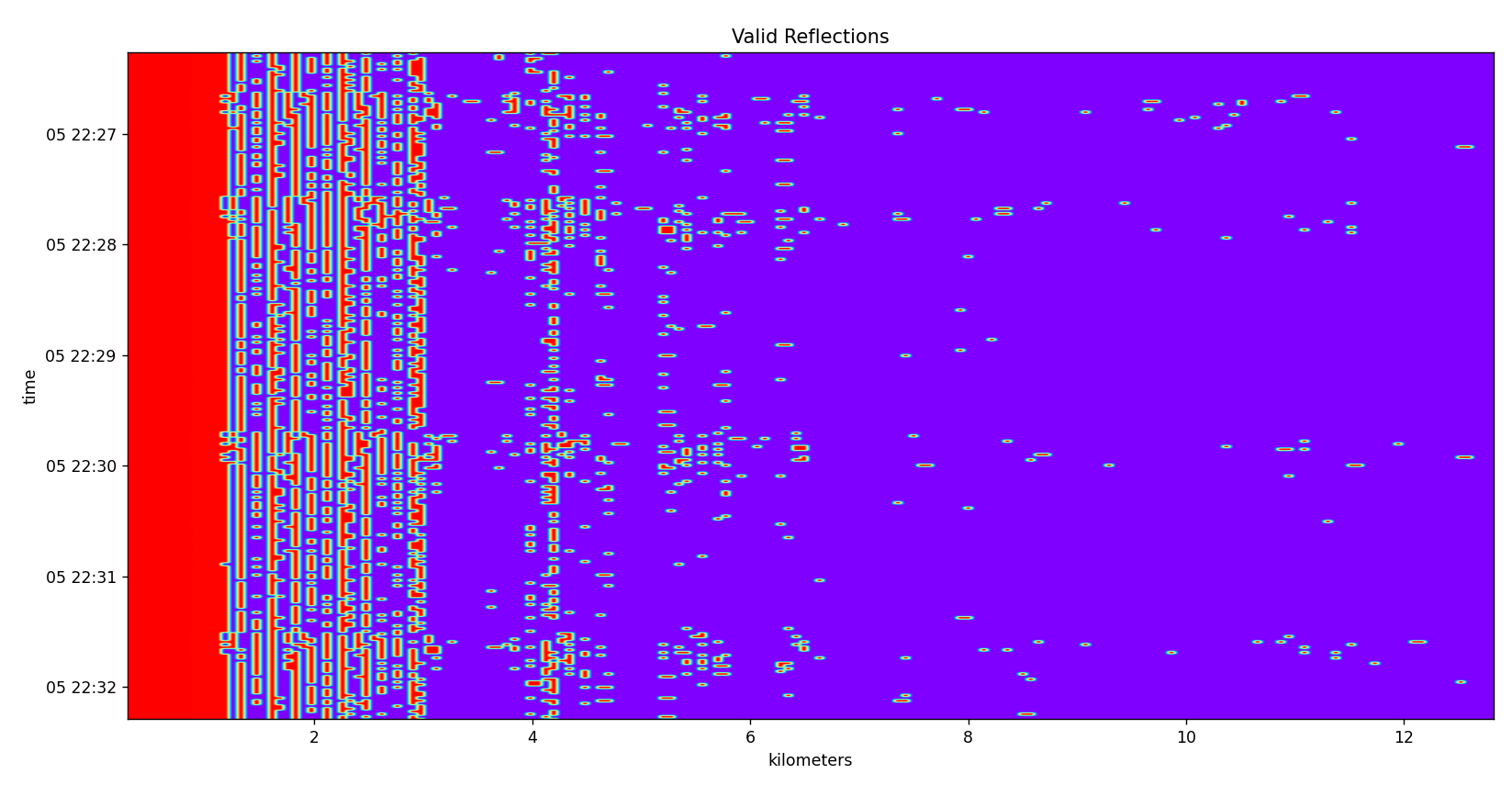
This is an interesting view. It is a function of the mag and phase. I first take the phase delta which has been showed in previous plot. I then do phase_delta > np.pi * 0.90 as a hard cutoff/filter for the magnitude. Anything less than that specified phase jump is set to zero which I hope throws out a lot of the noise and, if it works as intended, it leaves behind the signal shown above.
Could that be the cloud structure? Who knows. It looks cool and needs to be proven.
I had an idea. It may depend on chirp duration. A lot of the literature I’ve read didn’t speak a lot about what might be term really long chirp durations. Now, if I imagine a particle say of water in vapor form or anything radio reflective then I would also imagine it would be moving. I don’t see much sitting still for a 5 second duration. In order to produce a reflection at a specific point in time there would need be a reflection from a fixed point for a duration of 5 seconds and any movement would cause a loss of SNR.
This might be why I get certain features and not others.