The last test was a failure, so the parameters were adjusted. This time the sampling rate was reduced. I don’t think I talked about it, but I had used a new method in the last test that repeated the chirp. This new method is used and is center stage for hopefully increasing the SNR and getting some results.
The idea behind repeating is the chirp is based on the fact that the BladeRF card has phase noise creating a bound on the frequency stability. For example, if the resolution is around 1e3-hertz then we might say making smaller frequency transitions than 1e3-hertz per sample in the linear chirp only serves to mainly make the chirp longer because it causes at least two samples to overlap in the correlation. This whole idea creates a bound on the maximum chirp duration because we have finite bandwidth – bounded by the samples per second.
With a single chirp the distance is only limited by the duration between chirp starts or head-to-head not tail-to-head. In this case, with such low power and with the current chirp durations it is unexpected to ever use that much distance so repeating the chirp limits the maximum distance to the chirp’s number of samples (duration) which as I said in this case is fine. The number of repeats, in my intuition, does not seem to cause any trouble except for a longer duration and more expensive correlation.
The correlation is a problem because when using the FFT method it consumes a large amount of memory with large chirp durations and receive durations. The conventional correlation method is too slow. I suspect I could perhaps break down the FFT method and find a way to do just a partial correlation but that is only a guess.
In any case, the new method offers a longer chirp without creating overlap between the samples. The overlap would have greatly reduced the resolution perhaps to the point of being useless which might have been a problem in past tests.
Some Data
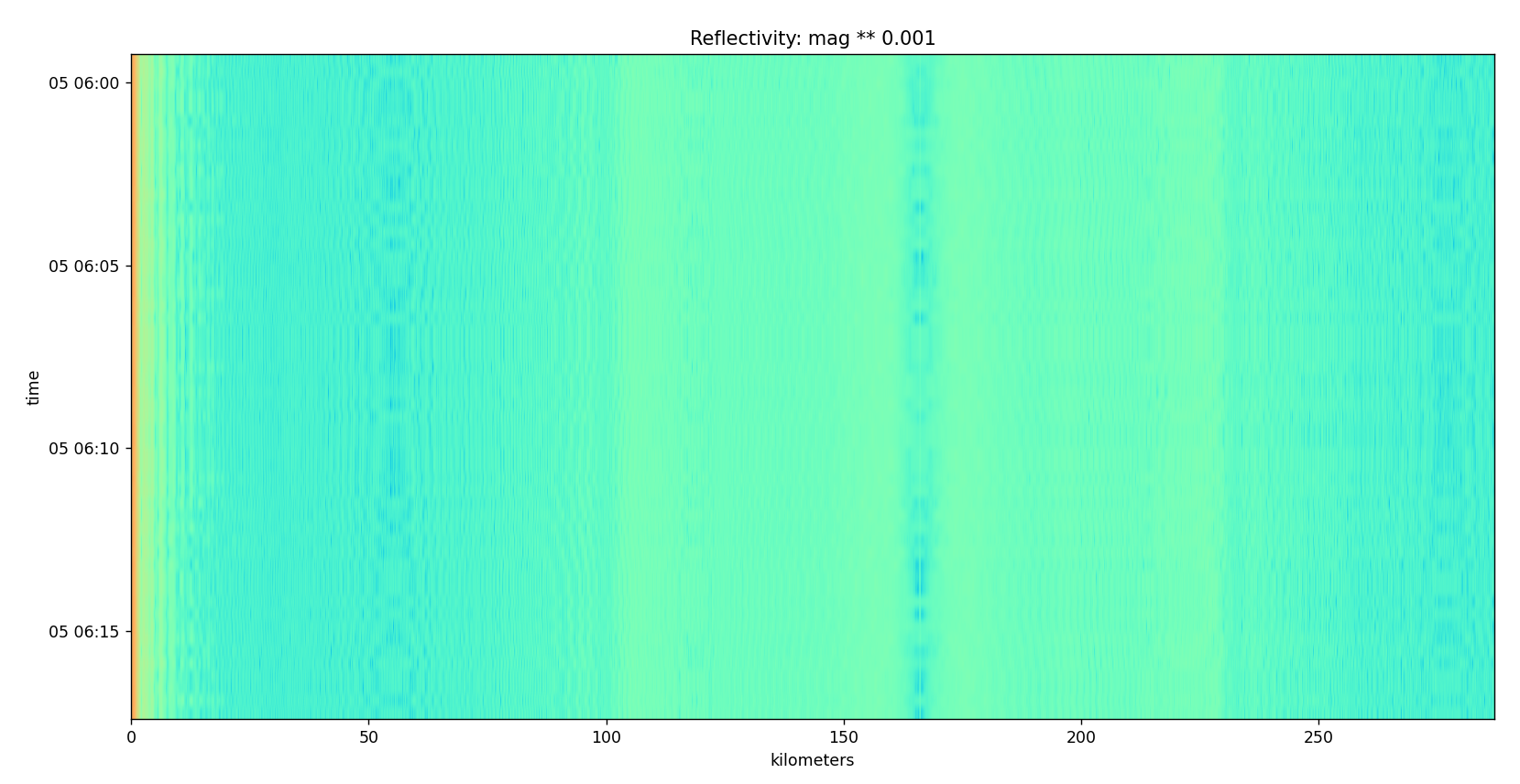
The above is the mag ** 0.001 plot. There are some features in it. The most profound is the strip at 165km and then the very large band behind it from 100km to 228km. There is another strip around 55km. The usual burst of energy from 0km to some point that is difficult to discern.

Here is a zoomed in view from 0km to 60km. You can see the burst of energy from 0km to 1.89km then a small gap and finally a number of small bursts as bands. Interestingly around 13km there are some bands which appear to be broken up in duration.
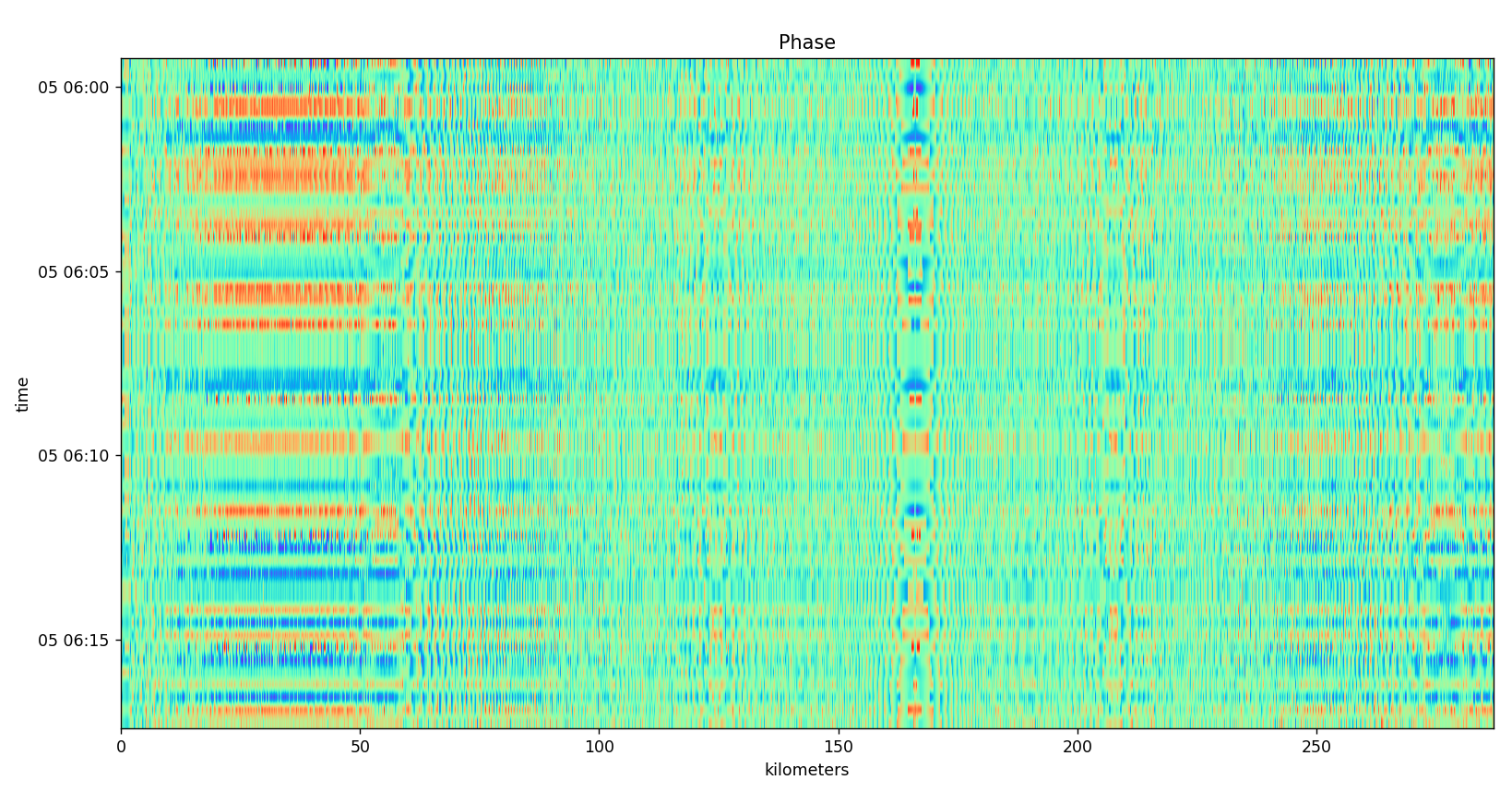
Here is the phase plot. Each row seems to start at a different phase offset but they all seem to display the same general pattern. One thing I do like is that there does not seem to be any degeneration into noise towards the end. Perhaps the signal made it all the way? If only it would bounce off some water vapor along the way!
At first glance, as usual, the data looks very interesting. There are obviously some factors at play here. I can’t figure out exactly what causes the banding on any of the past tests including this one, but it is obvious it exists, and it does not exhibit any kind of autocorrelation pattern I’d expect from a linear chirp. The only thing to do is wait and see if any changes happen that correlate with the weather.
Code
Since I have time while waiting for the data to be collected, I thought I’d include the code used by acquisition of the data.
import bladerf
import time
import queue
import threading
import numpy as np
import scipy.signal as signal
import pickle
import random
def do_chirp_loop(
factor=1,
samps_factor=1,
samps_rep=1,
sig_mag=2000,
tx_gain=42,
rx_gain=60,
bw=400e3,
cbw=390e3,
out_count=200):
"""Perform the chirp loop saving the output to a file.
The base SPS is 520834. To derive the actual SPS multiply the base SPS
by the `factor`. The `samps_factor` is how many seconds the chirp lasts
and can be fractional. The `samps_rep` is the point at which the chirp
repeats, it is in seconds, and can be fractional. The `sig_mag` is the
int16 positive maximum magnitude of the I or Q channel. The `bw` is
used with `dev.set_bandwidth` and sets the pass bandwidth on the board
while `cbw` sets the chirp bandwidth across DC.
"""
dev = bladerf.BladeRF(f'libusb:serial=5bb')
num_buffers = 32
buffer_size = 1024 * 8
buffer_byte_size = num_buffers * buffer_size
[dev.set_gain_mode(ch, bladerf.GainMode.Manual) for ch in [0, 1, 2, 3]]
dev.set_gain(0, rx_gain)
dev.set_gain(2, rx_gain)
dev.set_gain(1, tx_gain)
dev.set_gain(3, tx_gain)
sps = 520834 * factor
[dev.set_sample_rate(ch, sps) for ch in [0, 1, 2, 3]]
#dev.set_sample_rate(0, sps)
if bw is None:
bw = sps
[dev.set_bias_tee(ch, False) for ch in [0, 1, 2, 3]]
[dev.set_bandwidth(ch, bw) for ch in [0, 1, 2, 3]]
for ch in [0, 1, 2, 3]:
print('[%s] sps' % ch, dev.get_sample_rate(ch))
print('[%s] bw' % ch, dev.get_bandwidth(ch))
print('[%s] gain' % ch, dev.get_gain(ch))
#print('[%s] freq' % ch, dev.get_frequency(ch))
dev.sync_config(
bladerf.ChannelLayout.RX_X1,
bladerf.Format.SC16_Q11,
num_buffers=num_buffers,
buffer_size=buffer_size,
num_transfers=16,
stream_timeout=20000
)
rx_channel_count = 1
dev.sync_config(
bladerf.ChannelLayout.TX_X1,
bladerf.Format.SC16_Q11,
num_buffers=num_buffers,
buffer_size=buffer_size,
num_transfers=16,
stream_timeout=20000
)
[dev.enable_module(ch, False) for ch in [0, 1, 2, 3]]
[dev.enable_module(ch, True) for ch in [0, 1]]
rx_q = queue.Queue()
tx_q = queue.Queue()
#rx_t = threading.Thread(
# target=rx_thread,
# args=(dev, rx_q)
#)
#rx_t.start()
tx_t = threading.Thread(
target=tx_thread,
args=(dev, tx_q, buffer_byte_size),
daemon=True
)
tx_t.start()
samps = int(sps * samps_factor)
t = samps / sps
cycle = 0
def linear_chirp(freq_0, freq_1, samps, sps):
t = samps / sps
theta_step_start = np.pi * 2 * freq_0 * t / samps
theta_step_stop = np.pi * 2 * freq_1 * t / samps
theta = np.add.accumulate(np.linspace(theta_step_start, theta_step_stop, samps))
sig = np.exp(1j * theta)
return sig
assert bw <= sps
assert cbw < bw
bwp = 0.9
method = 'linear'
t = np.linspace(0, samps_factor, int(samps_factor * sps))
chirp0_i = signal.chirp(
t, -cbw, samps_rep, cbw, method=method
)
chirp0_q = signal.chirp(
t, -cbw, samps_rep, cbw, phi=90,
method=method
)
chirp0 = chirp0_i + 1j * chirp0_q
del chirp0_i
del chirp0_q
while True:
f_sig = np.zeros(samps * 2, np.int16)
f_sig[0::2] = chirp0.real * sig_mag
f_sig[1::2] = chirp0.imag * sig_mag
#f_sig[2::4] = chirp0.real * sig_mag
#f_sig[3::4] = chirp0.imag * sig_mag
f_sig = f_sig.tobytes()
lo_freq = random.randint(
int(400e6),
int(1e9)
)
lo_freq = 3.324e9
#lo_freq = 594221754
[dev.set_frequency(ch, lo_freq) for ch in [0, 1, 2, 3]]
time.sleep(0.25)
print(f'rxing for {int(sps * samps_factor * 1.5) / sps} seconds')
tx_q.put((f_sig, 0.125))
rx_samps = int(sps * samps_factor * 1.5)
if rx_samps < sps:
rx_samps = sps
rx_q.put(rx_samps)
rx_thread(dev, rx_q, rx_channel_count, buffer_byte_size)
#tx_thread(dev, tx_q)
rx_buf = rx_q.get()
rx_buf = np.ndarray(len(rx_buf) // 2, buffer=rx_buf, dtype=np.int16)
rx_buf = rx_buf.astype(np.float64)
b0 = rx_buf[0::2] + 1j * rx_buf[1::2]
print('building c0')
c0 = signal.correlate(b0, chirp0, mode='valid')
i = np.argmax(np.abs(c0))
c0 = c0[i:i+out_count]
print('building c1')
#c1 = signal.correlate(b0, chirp1, mode='same')[i:i+out_count]
c0_max = np.max(np.abs(c0))
#c1_max = np.max(np.abs(c1))
print('freq', lo_freq)
with open('test.signal', 'ab') as fd:
pickle.dump((sps, lo_freq, time.time(), c0, None), fd)
del c0
cycle += 1
def rx_thread(dev, q, channel_cnt, buffer_byte_size):
samps = q.get()
buf = bytes(4 * samps)
print('[RX] started', samps)
pre_buf = bytes(buffer_byte_size)
# drain the old data out of the buffer
dev.sync_rx(pre_buf, buffer_byte_size // 4)
# pull the new data out
dev.sync_rx(buf, samps * channel_cnt)
print('[RX] ended')
q.put(buf)
def tx_thread(dev, q, buffer_byte_size):
post_data = bytes(buffer_byte_size)
while True:
work = q.get()
if work is None:
break
data, delay = work
time.sleep(delay)
print('[TX] started', data[0:8])
dev.sync_tx(data, len(data) // 4)
# make sure the TX data fully flushes out
# by filling the buffers with zeros
dev.sync_tx(post_data, len(post_data) // 4)
print('[TX] ended')
if __name__ == '__main__':
base_sps = 520834
factor = 4
samps_mul = 10000
do_chirp_loop(
factor=factor,
out_count=4000,
samps_factor=0.001 * samps_mul,
samps_rep=0.001,
tx_gain=60,
bw=base_sps * factor,
cbw=base_sps * factor * 0.45
)Then of course the code used to produce the graphs:
import pickle
import numpy as np
from scipy import signal
import matplotlib.pyplot as plt
import matplotlib.dates as mdates
from lib.general import *
import scipy.ndimage as ndimage
import datetime as dt
def linear_chirp(freq_0, freq_1, samps, sps):
t = samps / sps
theta_step_start = np.pi * 2 * freq_0 * t / samps
theta_step_stop = np.pi * 2 * freq_1 * t / samps
theta = np.add.accumulate(np.linspace(theta_step_start, theta_step_stop, samps))
sig = np.exp(1j * theta)
return sig
if __name__ == '__main__':
phase = []
phase_cor = []
mag = []
f = []
ts = []
o = []
freq_low = None
freq_high = None
sps = None
c0_offset = 0
k = []
with open('test.signal', 'rb') as fd:
ndx = 0
while True:
try:
_sps, freq, _ts, c0, offset = pickle.load(fd)
c0 = c0[c0_offset:]
if sps is not None:
assert sps == _sps
sps = _sps
if freq_low is None or freq < freq_low:
freq_low = freq
if freq_high is None or freq > freq_high:
freq_high = freq
print(freq, offset)
#c0 = c0[::10]
except EOFError:
print('eof error')
break
#o.append((freq, c0))
f.append(freq)
ts.append(dt.datetime.fromtimestamp(_ts))
phase.append(np.angle(c0))
mag.append(np.abs(c0)[1:])
phase = np.array(phase)
phase_cor = np.array(phase_cor)
mag = np.array(mag)
x_lims = mdates.date2num(ts)
def do_imshow(v, title, begin_offset=0):
fig, ax = plt.subplots()
ax.imshow(
v, # ** 0.001,
extent=[
299e6 / sps * begin_offset * 0.5 / 1e3,
299e6 / sps * v.shape[1] * 0.5 / 1e3,
x_lims[-1],
x_lims[0]
],
aspect='auto',
cmap='rainbow')
ax.yaxis_date()
plt.title(title)
ax.set_ylabel('time')
ax.set_xlabel('kilometers')
plt.show()
mag_mean = np.mean(mag, axis=0)
dmag = np.abs(mag[1:, :] - mag[:-1, :]) ** 0.001
do_imshow(
ndimage.gaussian_filter(dmag[:, 0:], 10),
'Reflectivity: np.abs(mag[1:, :] - mag[:-1, :]) ** 0.001',
begin_offset=0
)
do_imshow(mag ** 0.001, 'Reflectivity: mag ** 0.001')
do_imshow(phase, 'Phase')Conclusion
The test was a failure. The clearing of clouds, rain, and weather conditions elicited no response from the output. It was determined that the reflections present in the data were not from the clouds.