In these tests I switched out the antennas to two log-periodics, only sent a single chirp, and increased the sampling rate to around 16-msps. The parameters are as follows:
Parameters: factor=32, out_count=8000, samps_factor=5, tx_gain=52, bw=4000000The samps_factor was changed to represent the whole or fractional number of seconds. In this case, the chirp is 5 seconds long. The bandwidth was changed to 4-mhz which places the chirp at -3.6mhz to -10khz. I just realized I made a mistake because the chirp should have been from -1.8mhz to -10khz. This might be okay because the chirp likely abruptly wrapped around. I will have to correct it later since the test is already underway.
I also had to upgrade to a computer with more RAM to deal with the increasing sampling rate.
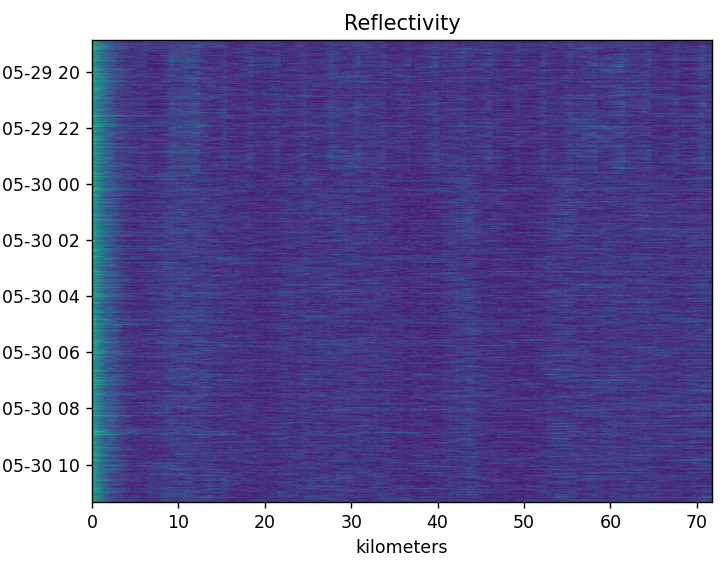
The above is the output from the magnitude of the correlation against the chirp. There is some energy at the beginning which rapidly falls off. There is some banding that is hard to see.
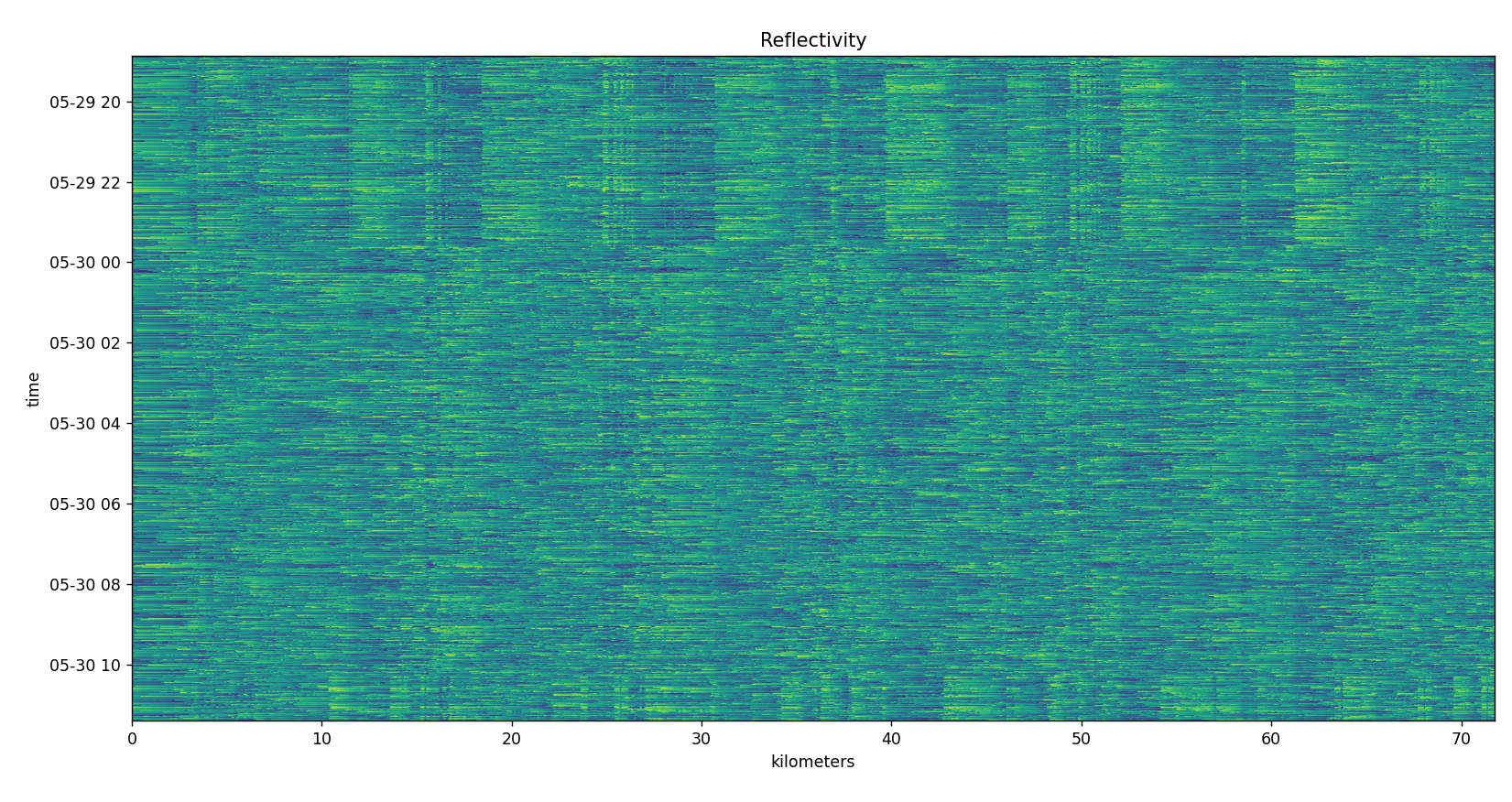
The above is phase. It used np.angle(correlation_output). It may be hard to see but what is visible is the phase is rotating clockwise at a consistent pace. The reason it looks like noise is because the starting phase is different for each row in the output. The next image will show the consistency of this rotating phase.
As can be seen in the above image, there is a constant color. If one zooms in there are some discontinuities but they are averaged out in the above image simply from the oversampling. The above image data was generated by taking the phase difference of each subsequent sample such that what is being seen is the phase delta between samples. The instantaneous phase.
Now, I think it is important here because what I predicted and expected was that each reflection would be advanced in phase more than the last due to the phase of the signal itself having advanced over the distance it travels from the last reflection.
The only problem is that np.mean(phase) gives a value of -5.09e-19 which is much too small. However, spot checking the above image produces values such as 0.02, -0.005 and such forth which are more realistic and all fall within the range of 53khz, -13khz, and so forth more consistent with the phase increment I’d expected.
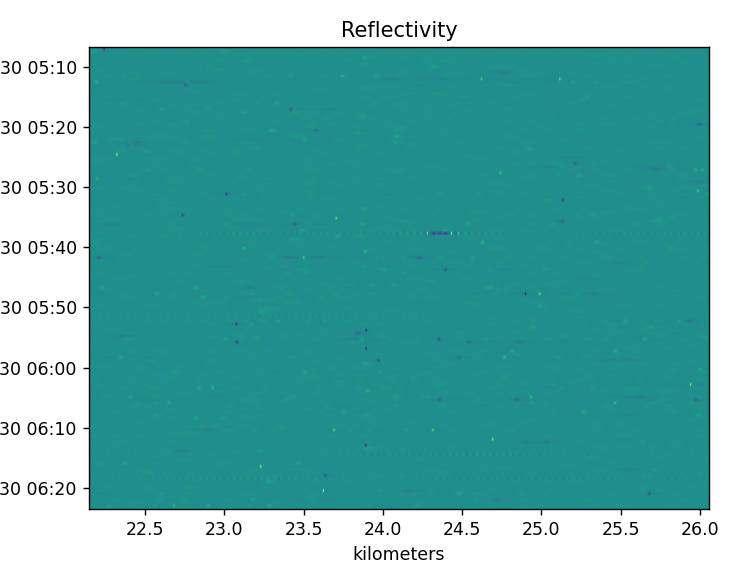
The above image shows a zoomed in view of the phase delta. You can see that it only appears to be completely constant. There are small blips and little runs of turbulence/ringing where the phase seems to oscillate.
Now, taking a pattern against the above. A pattern such as this:
pat = np.array([
[-0.22, -0.12, 0.27, 0.22, -0.14, -0.22, -0.22, -0.12, 0.27, 0.22, -0.14, -0.22],
[-0.22, -0.12, 0.27, 0.22, -0.14, -0.22, -0.22, -0.12, 0.27, 0.22, -0.14, -0.22],
[-0.22, -0.12, 0.27, 0.22, -0.14, -0.22, -0.22, -0.12, 0.27, 0.22, -0.14, -0.22],
])This pattern is basically a mimic of the up and down nature of some of the artifacts seem in the zoomed in view. Then using a correlation with this pattern, we get the following output.
Taking the absolute value of the above produces the following.
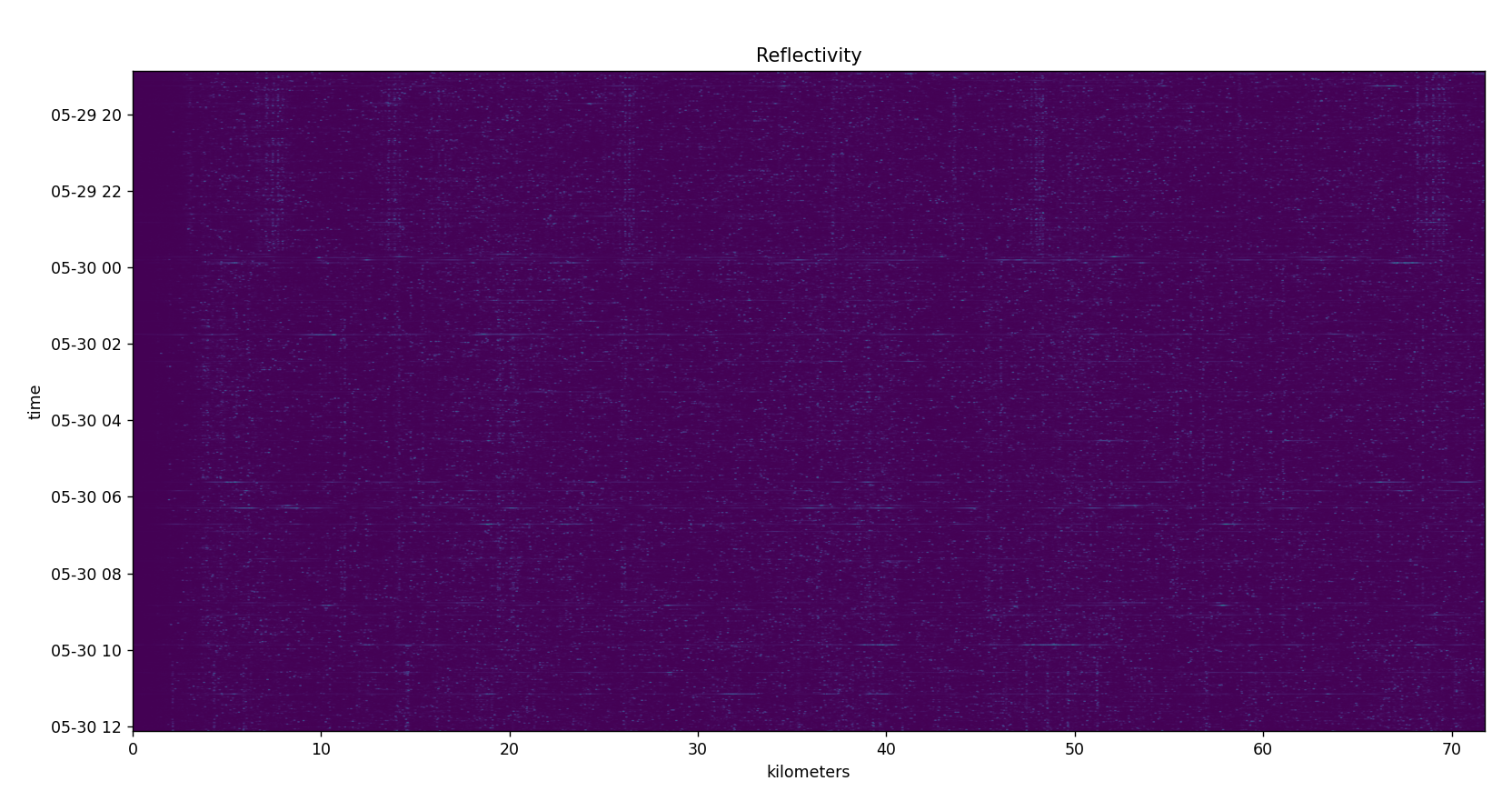
Now, those vibrations within the phase are more visible.
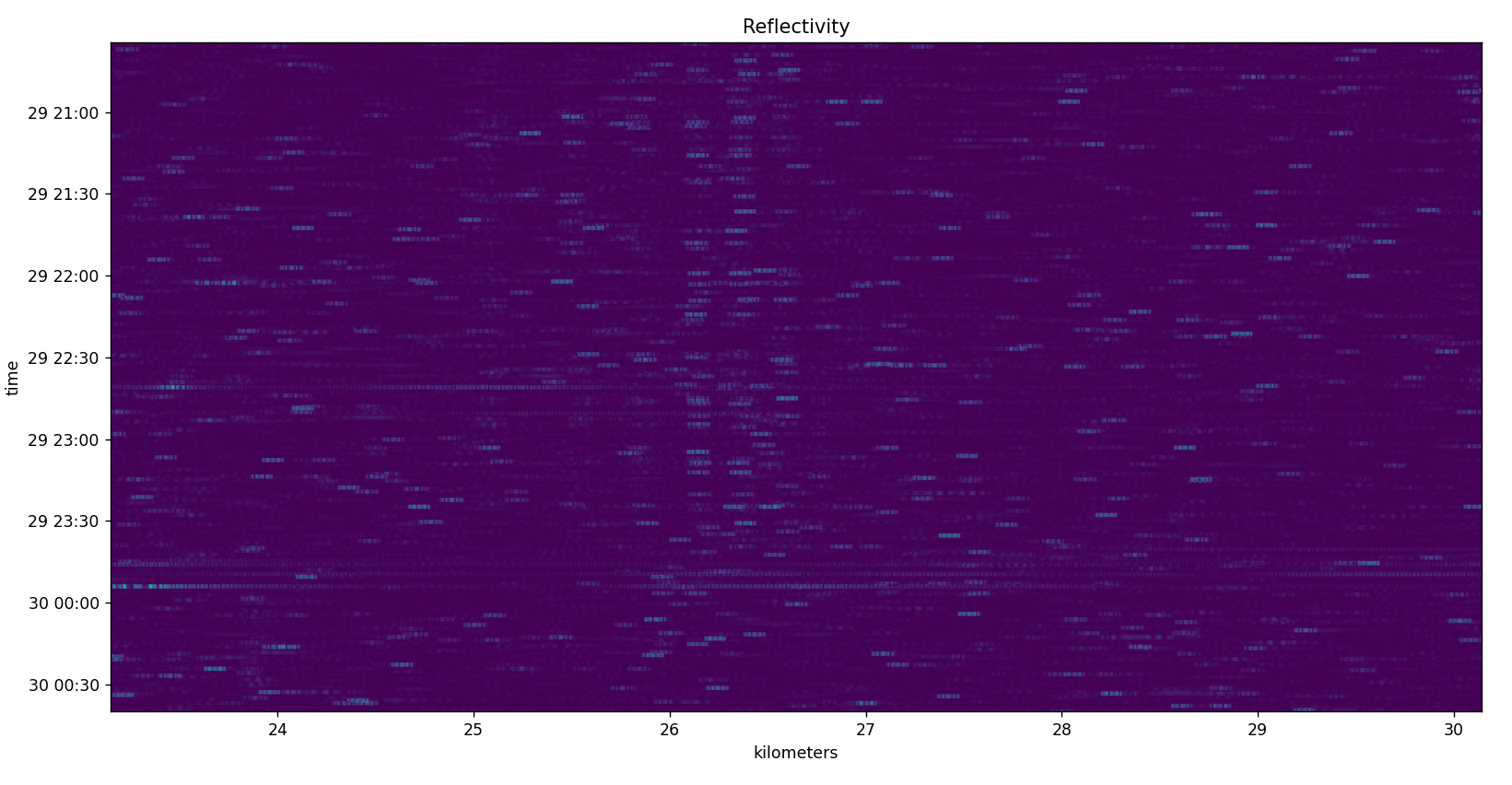
Zoomed in the np.abs(signal.correlate(phase_delta, pattern, mode='valid')) looks like the above. With some Gaussian smoothing/filtering it looks like the following.
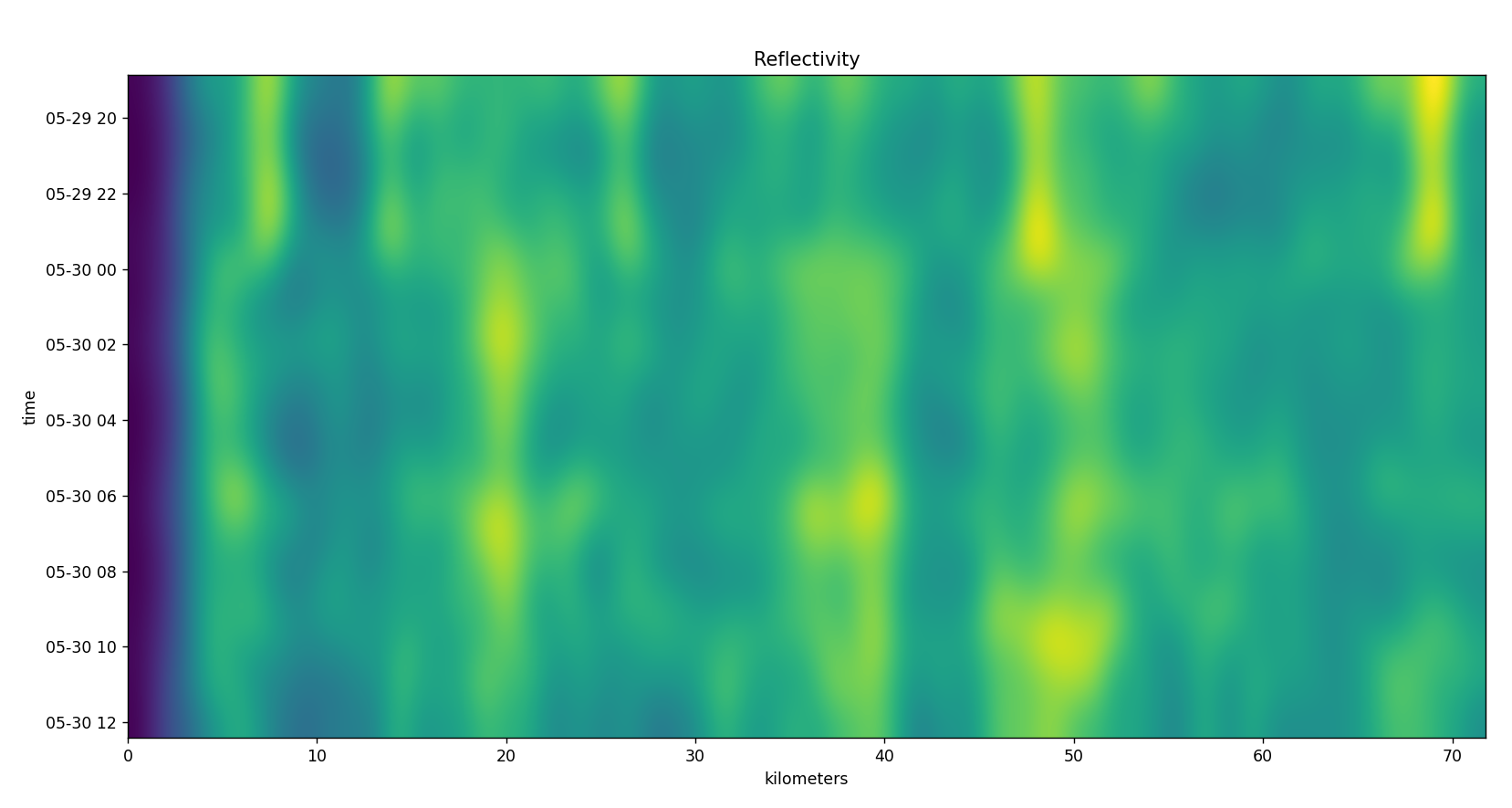
The above is with scipy.ndimage.gaussian_filter(data, sigma=100).
I find the last output very interesting. I think it paints a better picture of where these phase vibrations are location at and the density. They were next to impossible to see with the raw phase, but they appear to be concentrated in bands that have gradual changes in altitude.
I should talk more about the phase itself. There is some matching with the correlation magnitude, the first image shown. The exact cause of these vibrations within the phase I am not sure about.
I can only imagine that perhaps as the signal enters into a concentration of impedance turbulence it too produces turbulence in the received phase. I might expect a cloud or some formation of ions in the atmosphere to be non-homogenous such that as the signal traveled through this collection of particles it might experience an up and down in impedance. The collection of particles may not present a smooth bi-directional transition. There are obviously many places where the pattern highlighted blips in the phase too.
These blips were single or small places where the phase abruptly jumped forward or backward and then afterward resumed its normal phase delta. These obviously must be areas where there is a single major impedance change.
The sampling rate in this experiment is about 16,666,688-hertz which yields about 17.93-meters per sample. It would seem to me that the received phase depends on the amount of energy reflected during this period at a particular phase and the duration. An integration of sorts must happen during this period. That makes it difficult to say if there was a 17.93-meter long region of gradual impedance change that produced the phase deviation or there was a small 1-meter long cross-sectional region. I think this is just the nature of the beast. The resolution with the current sampling rate can’t be much better.
I feel that the interesting part is that there is something there as long as the experiment is actually receiving the signal and this data isn’t a manifestation of some internal process of the circuit or some shaping of random noise. It means that there are regions in the atmosphere that are different in electrical impedance.
I also think the reason the raw phase isn’t aligned per row has to do with the local oscillator in the transmitter and receiver mixer. I believe the type of mixer is a switching one that uses a square wave. I can’t be sure, but I believe I can still use the model of an ideal mixer and especially a digital one.
So, if I do that, then what happens is the phase of the LO (local oscillator) causes the incoming signal to be rotated accordingly. This rotation is dependent on the timing of the receive and since I don’t synchronize but use a more ad-hoc timing system I get a different phase each time causing each row of the raw phase to start at a different phase. This I believe is why the phase delta is so consistent, constant yet the actual absolute phase is not.
The same may also happen on the transmitter side. The signal goes out starting at phase zero but then gets rotated by the mixer and then rotated again by the receiving mixer. Of course, the physical channel (the sky) impacts a consistent and constant rotation as the wave travels and then the impedance mismatches impart these phase jumps.
Now, the only thing left to do is to wait and see if some changes happen consistent with actual weather or atmospheric changes.