Spurts
I was examining the output from a long run at about 35-msps. These usually run at a much lower sampling rate at around 1-msps or a few million. I kept seeing these strange reflections.
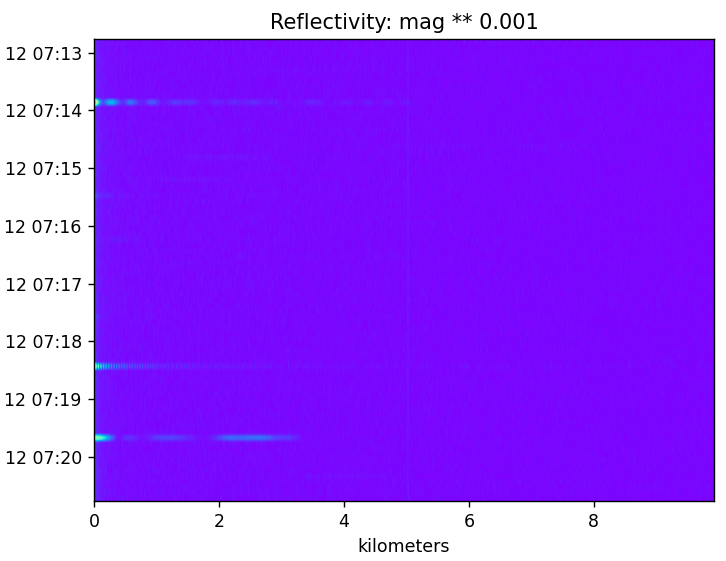



The spurts I might call them vary in form, but they all share the characteristic of beginning at altitude zero and extending some distance. Below is what the phase delta looks like.
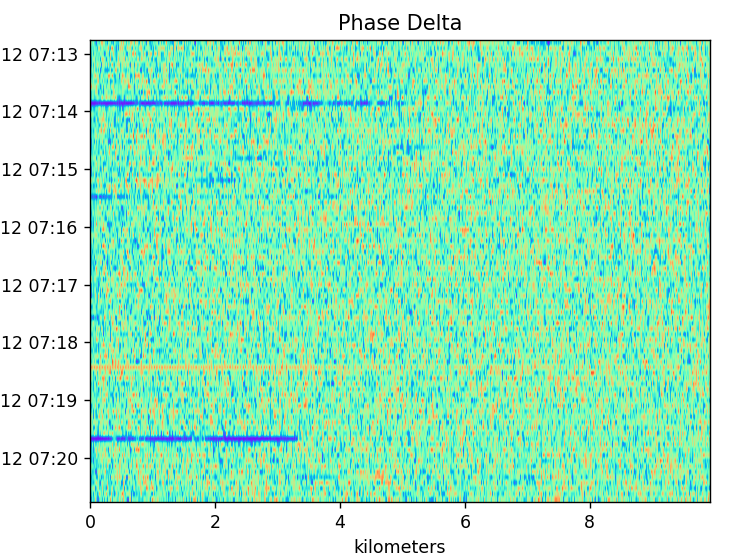
The phase delta has been continuous for all I have seen except the third there between 07:18 and 07:19. That one shows some ripple, and its phase is rotating much faster than usual.
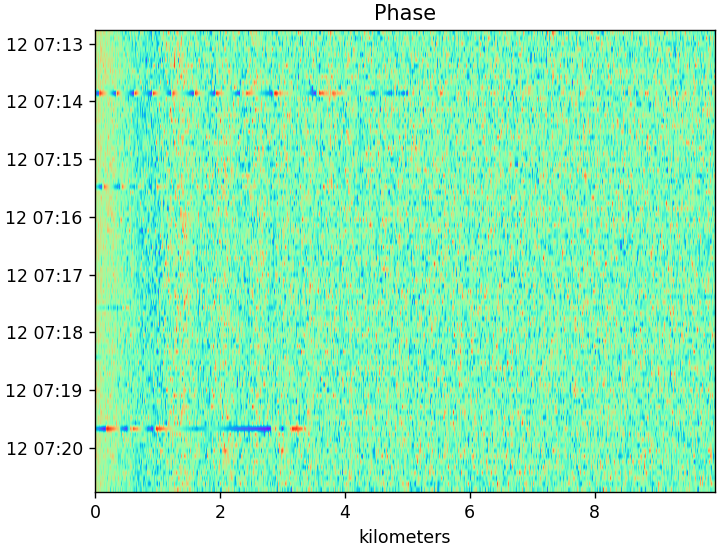
The view of raw phase shows a clearer picture. You can see that each spurt is not rotating consistently. In some cases, it changes.
I’m left not sure of what causes them. I’ve decided to move on to talking about stationary signal removal and leave these spurts for the future.
Stationary Signal Removal
I started using something I thought was interesting. I figured since my RX and TX are on at the same time and the fact that I should be capturing the initial chirp that I could in theory build up an image of the signal over time. For example, when I receive at the same time that I transmit, I do not just see the same signal I transmitted. Instead, I see a distorted form of it. It gets distorted by the noise, by the antenna elements, and such forth. It would be helpful to know exactly what the signal looks like because I could subtract it or even correlate with it and get a better SNR.
Stationary Signal Recovery
The way this works is first I correlate with the chirp to find the initial offset. Then, I extract a chunk starting from this initial offset and extending some number of samples – the chirp length if you would like. Each iteration I append this to a list and the find the signal minus the noise I do an average such as np.mean(list, axis=0) where list is the array of chunks. The idea here is that the signal of interest remains stationary as in it doesn’t change much but the noise will all average out to zero. Also important is hopefully all the distortions from the antenna will remain thus helping to improve the correlation or allow for subtraction of the signal.
For my first exploration, I decided to perform this function and dump the result at iterations 10, 100, and 1000. Below is the result of 10 iterations.
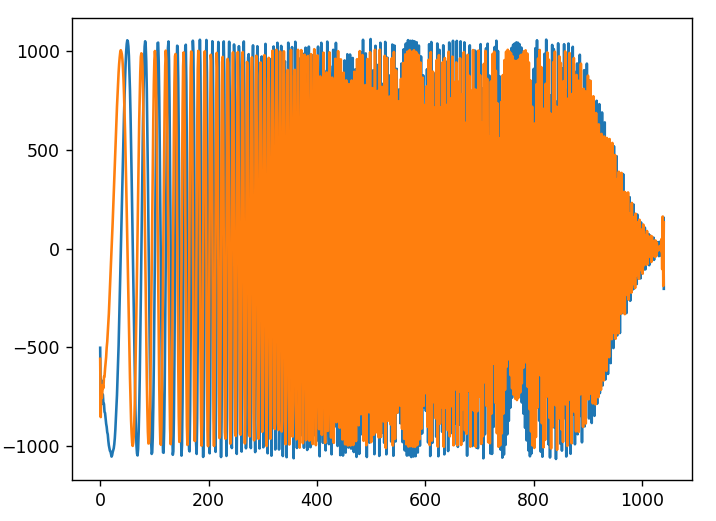
I can’t explain why there is this sudden lowering of the magnitude towards the end. The frequency will have been reaching a maximum or near the baseband edge which could account for that. As I said, this would be the distorted form of the chirp as seen by the RX side. The blue is the real component and the orange is the imaginary component of the quadrature signal.
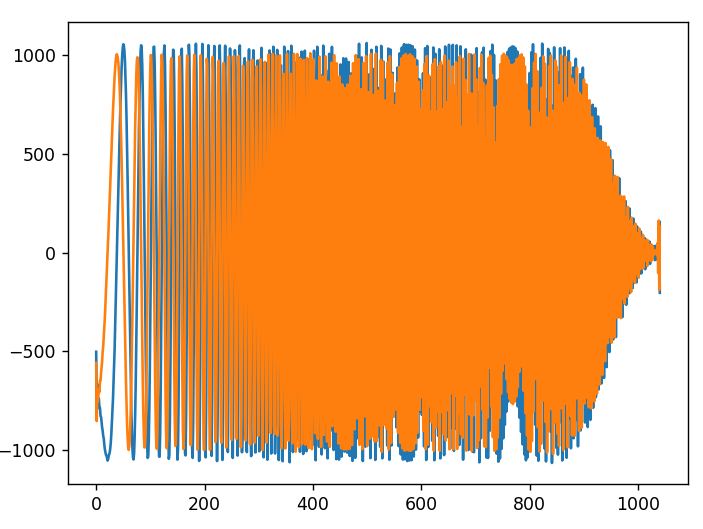
The image above is on the 100th iteration. There does not seem to be much change from the 10th iteration. This means we acquire the signal quite quickly which is good.
As you can see the recovery of the chirp appears to be successful. It has also brought to my attention the kind of distortion that is happening to the signal as it passes through all the channels. With this new information I think I can improve the system to gain some more signal to noise ratio.
Correlating with Recovered Chirp
Now, from here I went on to correlate with this recovered chirp instead of the synthetic chirp. The synthetic chirp is the one built with Numpy before it is sent over the wire. I also did the doppler shift function with the recovered chirp by simply shifting it up and down in frequency.
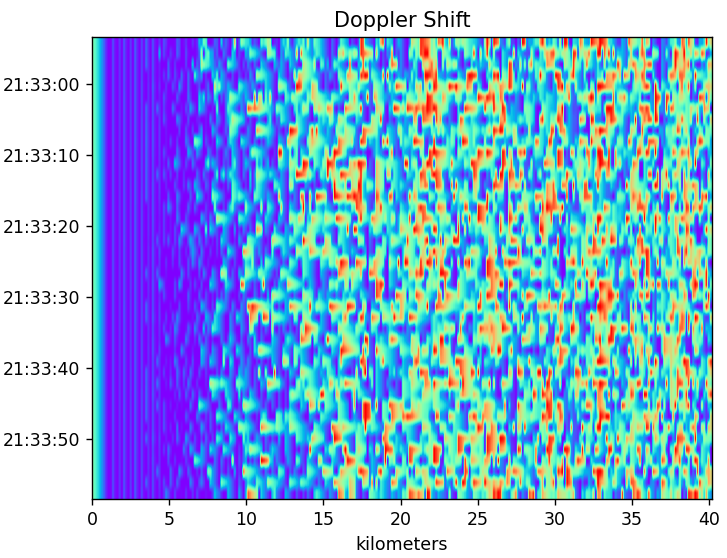
The above is the doppler shift output. It looks interesting. I have a gentle slope at the start and then what appears to be a fade into noise around 10km. The real test is if it changes over time.
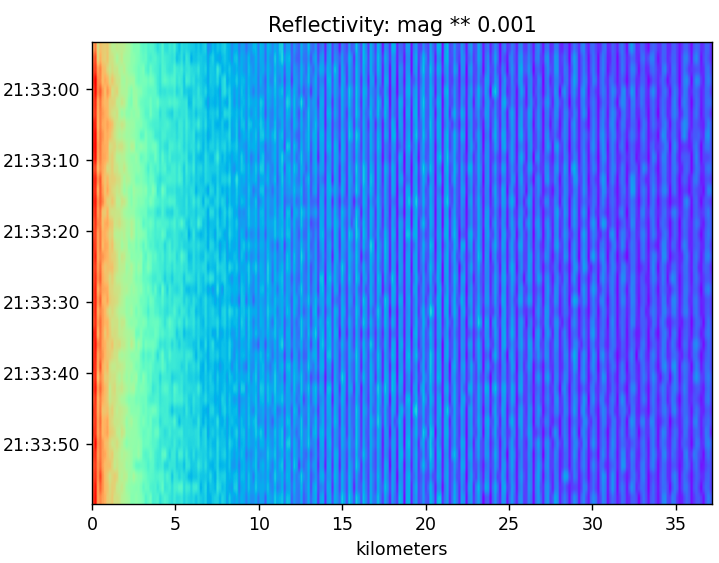
This is the reflectivity with a logarithmic function for scale. There is the high amount of reflection at the beginning with a decrease over time.
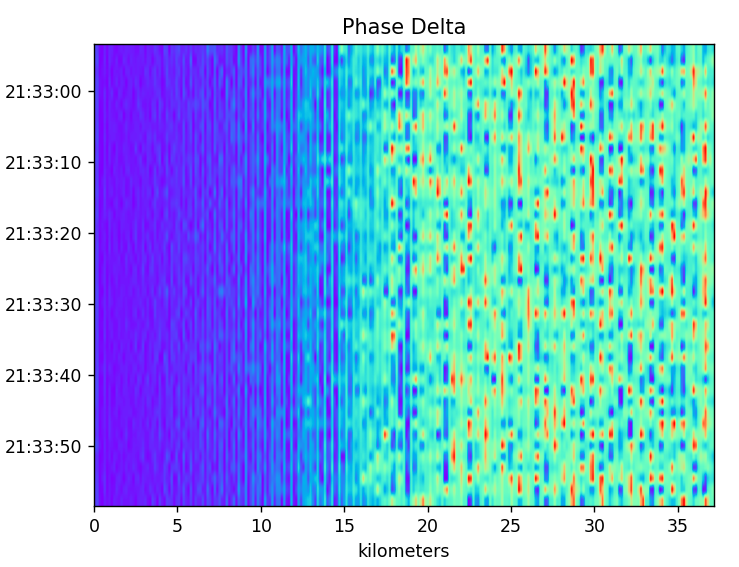
The phase delta plot also looks interesting. It shows a fairly consistent rotation of the phase up until about 13km and then around 15km it appears to succumb to the effects of noise.
My expectations are low. I’ve seen a lot of interesting results. The patterns created by the correlations can be interesting but have so far amounted to nothing more than the TX chirp itself. If there are reflections, I believe they will be far too weak to be detectable and they will be swamped to a degree by the TX signal making them even harder to recover.
It turned out this run didn’t yield anything interesting. The output remained constant and stationary. I decided to change things up in the next test/section.
Removal and Correlation
I’ve finally settled on the idea of removing the recovered chirp and only looking for doppler shift. The idea is that no particle is going to be sitting still unless its transversal velocity is exactly zero which is possible but should be rarer. So, looking for an exact replica is wasteful because no reflection I should be concerned with is going to be that. It also might clear up the output so I’m not seeing the autocorrelation of the chirp.
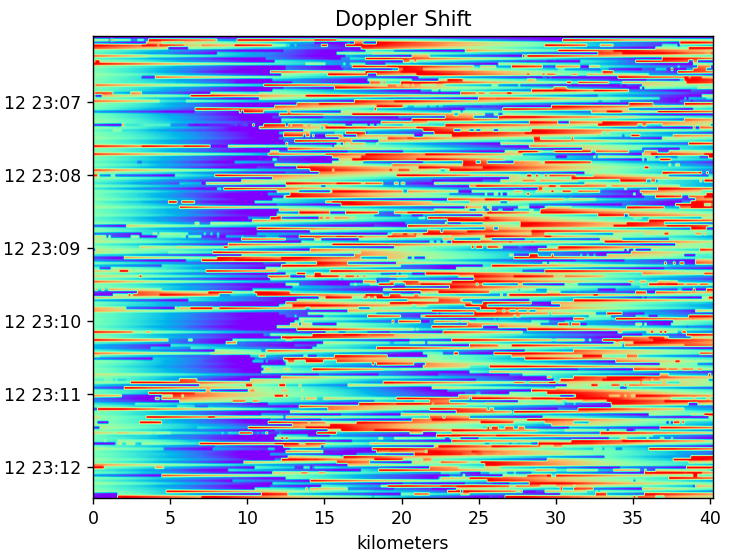
Okay, so the beginning is cleaned up a lot after subtracting the chirp out. I’m still getting this interesting boundary around 13km.
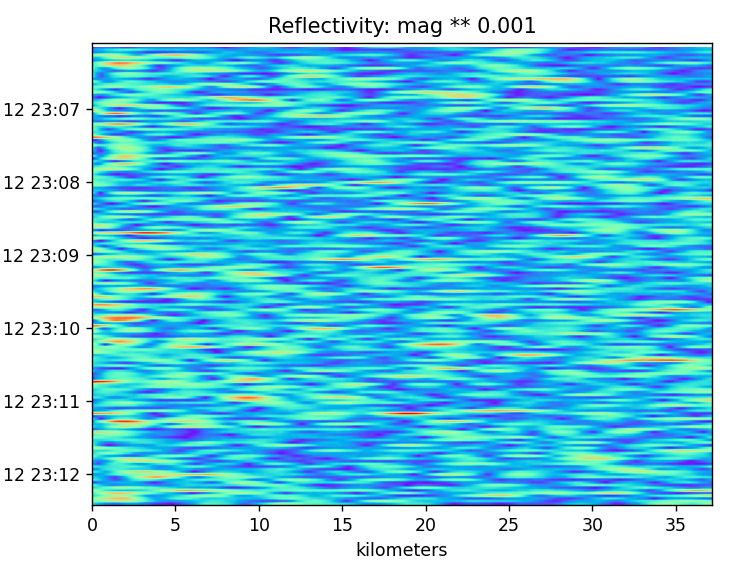
The reflectivity is mostly noise now. There are spots but I’m not sure of their cause.
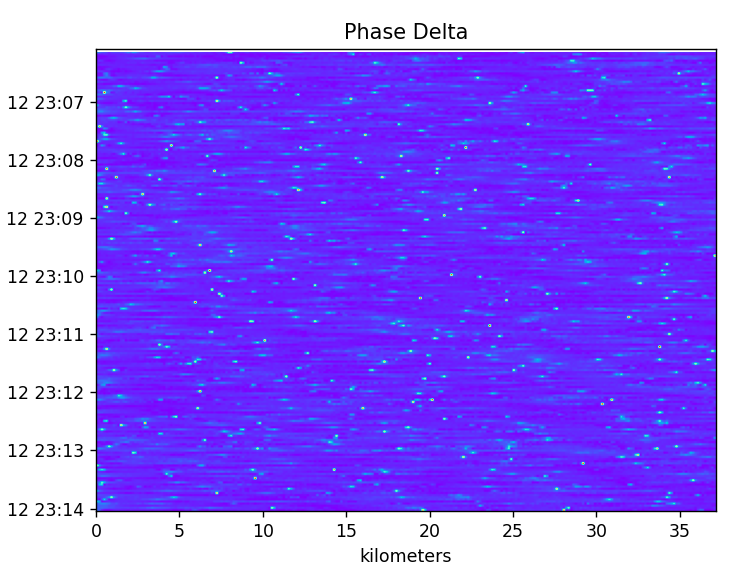
Interestingly, the phase delta isn’t chaotic as I’d expect. I’d think noise would produce a very noisy delta. The actual phase is showing very smooth transitions on average.
Correlation with Best Doppler Shift
Okay, the phase and phase delta are pegged to the zero shifted recovered chirp. Instead, let me see what I get if I output the phase of the best correlated frequency shifted version of the recovered chirp per sample. After all, we should want the best correlation which is likely to be frequency shifted.
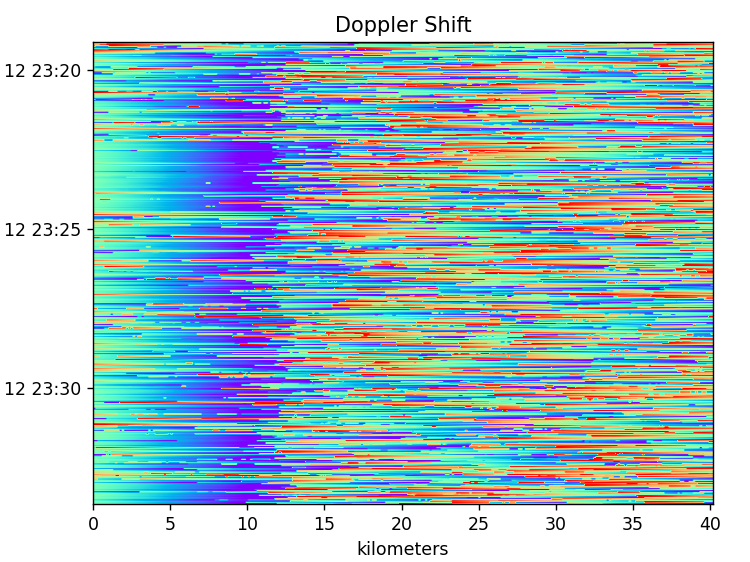
After making the above changes, I get the above output for the frequency/doppler shift. There is still that boundary around 13km. The doppler shift shows a motion towards us from ground level which picks up speed and finally around 13km descends into what appears to be noise. This could make sense from a weather system standpoint. I might expect to see significant downdraft which speeds slowing as it approaches the ground level.
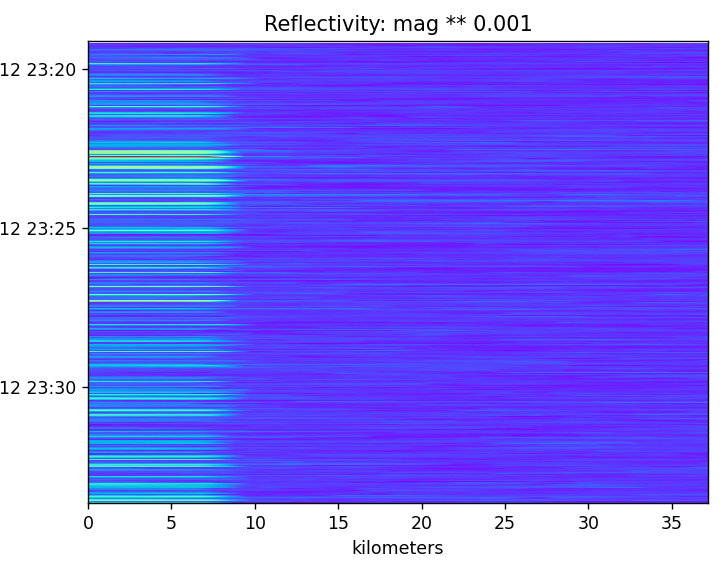
For reflectivity, I’m showing a very consistent return until about 9km. I’m not sure what to make of this. I’d expect it to fall off with distance, but this appear to not only remain constant but at some times there is no reflectivity.